Vật lý cổ điển
Xem thêmVật lý nguyên tử, phân tử và quang học
Xem Thêm
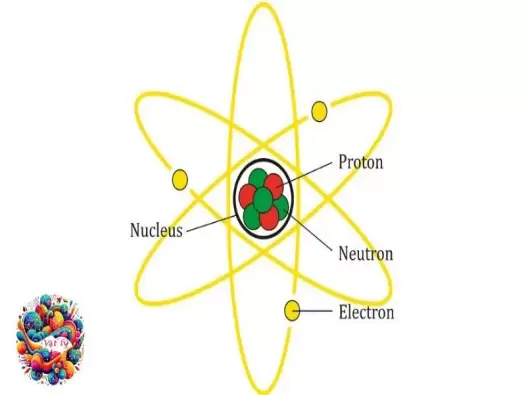
Mẫu nguyên tử Bo: Giải mã cấu trúc nguyên tử
Chào mừng bạn đến với vatly.edu.vn! Hôm nay, chúng ta sẽ tìm hiểu về mẫu nguyên tử Bo, một trong những mô hình cơ bản nhất của lý thuyết nguyên tử, được đề xuất bởi Niels Bohr. Mẫu này không chỉ làm sáng tỏ cấu trúc của nguyên tử mà còn giúp giải thích các hiện tượng quang phổ, đóng góp vào sự phát triển của vật lý hiện đại.

Tìm hiểu chi tiết về hiện tượng quang - phát quang
Chào mừng các bạn đến với vatly.edu.vn, nơi tìm hiểu và khám phá những hiện tượng vật lý thú vị. Hôm nay, chúng ta sẽ cùng tìm hiểu về hiện tượng quang-phát quang - một khái niệm không chỉ quan trọng trong nghiên cứu khoa học mà còn có nhiều ứng dụng trong đời sống và công nghệ.
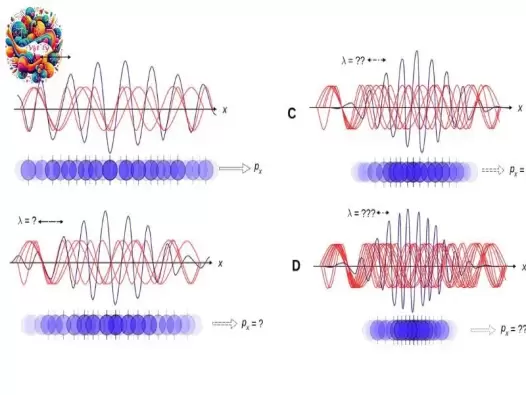
Giải mã chi tiết nguyên lý bất định Heisenberg
Nguyên lý bất định Heisenberg là một khái niệm nền tảng trong cơ học lượng tử, khẳng định rằng không thể đồng thời đo chính xác cả vị trí và động lượng của một hạt vi mô với độ chính xác tùy ý. Nguyên lý này có ý nghĩa quan trọng trong việc hiểu hành vi của các hạt vi mô, và đặt ra những giới hạn cho khả năng kiểm soát và dự đoán các hệ thống lượng tử.
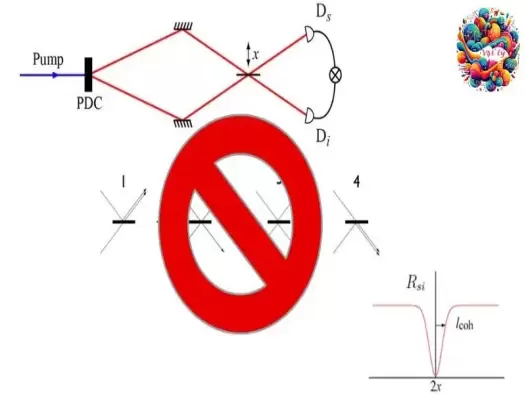
Khám phá hiệu ứng chồng chất và vướng víu lượng tử
Khám phá thế giới kỳ diệu của hiệu ứng chồng chất và vướng víu lượng tử - hai khái niệm cốt lõi giúp mở rộng hiểu biết của chúng ta về vũ trụ lượng tử và tiềm năng trong công nghệ tương lai.

Thí nghiệm khe Young và thí nghiệm con mèo Schrödinger
Khám phá sự kỳ diệu của cơ học lượng tử qua hai thí nghiệm nổi tiếng: Thí nghiệm khe Young giải thích về tính sóng của ánh sáng và thí nghiệm con mèo Schrödinger với cái nhìn sâu sắc về siêu vị trí.

Tìm hiểu về Spin electron - Số lượng tử bí ẩn của vật lý
Spin là một thuộc tính lượng tử cơ bản của các hạt như electron, proton, và neutron, đóng vai trò giống như một dạng “moment động lượng góc nội tại” của hạt. Trái ngược với moment động lượng góc trong vật lý cổ điển
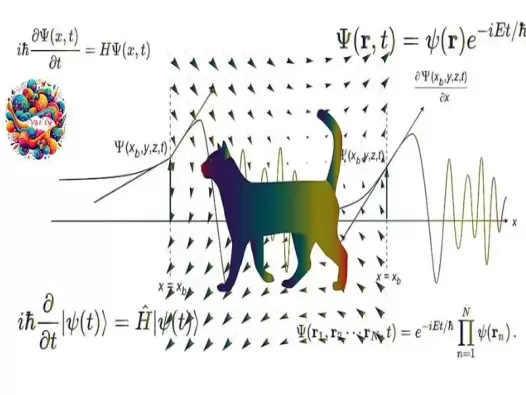
Giải mã bí ẩn về phương trình Schrödinger
Trong thế giới kỳ diệu của cơ học lượng tử, phương trình Schrödinger đứng như một biểu tượng của sự khám phá và hiểu biết. Được đặt tên theo nhà vật lý học Erwin Schrödinger, phương trình này không chỉ là cốt lõi của cơ học lượng tử mà còn mở ra những cánh cửa mới trong việc giải đáp các bí ẩn vũ trụ từ mức độ vi mô nhất.

Giải thích chi tiết các hiện tượng lượng tử
Trong thế giới vô hình của cơ học lượng tử, các hiện tượng lượng tử đặc biệt mở ra cửa sổ vào bản chất sâu sắc nhất của vũ trụ, nơi các quy luật cổ điển không còn áp dụng. Khám phá những bí ẩn của các hạt vi mô và hiểu biết về cách chúng tương tác là chìa khóa để giải mã vũ trụ, từ hạt cơ bản nhất đến thiên hà xa xôi.
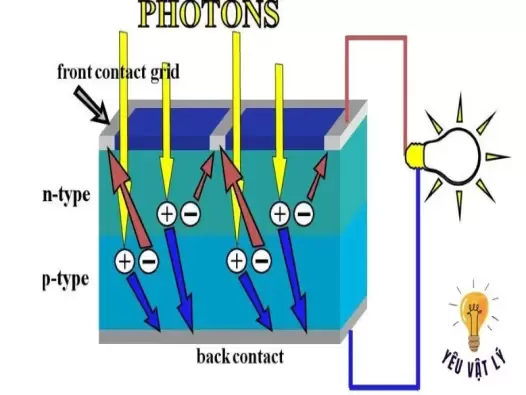
Hiện tượng quang điện trong: Giải thích, ứng dụng và kiến thức cần nắm
Trong thế giới đầy rẫy các hiện tượng vật lý hấp dẫn, hiện tượng quang điện trong đứng như một minh chứng kinh điển cho sự đơn giản mà sâu sắc trong việc hiểu biết và ứng dụng các nguyên lý vật lý cơ bản. Bài viết này sẽ đưa bạn đi sâu vào thế giới của hiện tượng quang điện trong, từ cơ sở lý thuyết đến các ứng dụng thực tế, giúp bạn khám phá và hiểu rõ hơn về một trong những hiện tượng vật lý thú vị và cơ bản nhất.
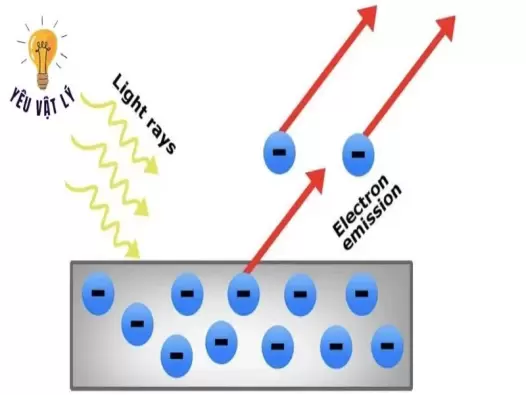
Chìa khóa giải mã hiện tượng quang điện
Trong thế giới đầy rẫy các hiện tượng vật lý hấp dẫn, hiện tượng quang điện đứng như một minh chứng kinh điển cho sự đơn giản mà sâu sắc trong việc hiểu biết và ứng dụng các nguyên lý vật lý cơ bản. Bài viết này sẽ đưa bạn đi sâu vào thế giới của hiện tượng quang điện, từ cơ sở lý thuyết đến các ứng dụng thực tế, giúp bạn khám phá và hiểu rõ hơn về một trong những hiện tượng vật lý thú vị và cơ bản nhất.
Danh Mục
Vật lý hạt nhân và hạt cơ bản
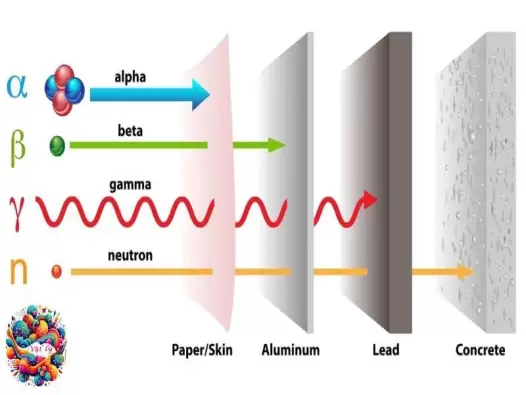
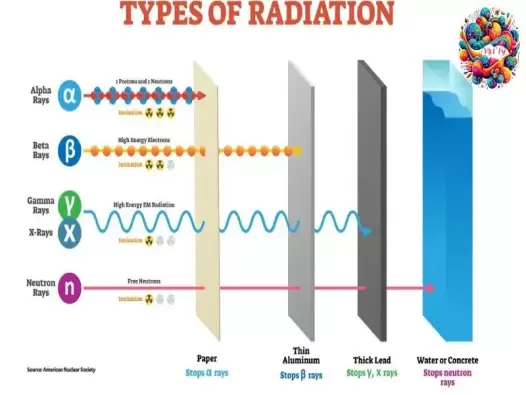
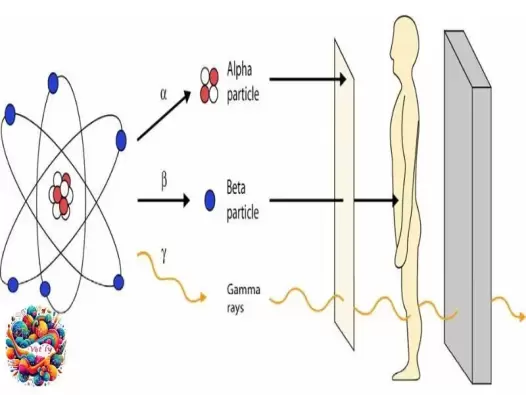
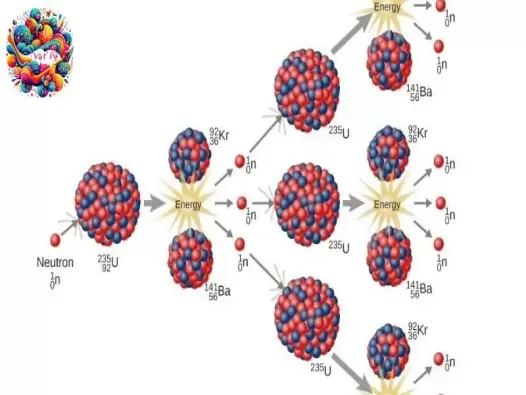
Khám phá bức xạ Alpha, Beta và Gamma









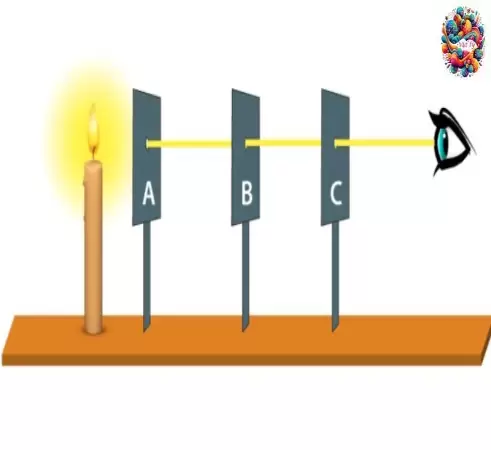
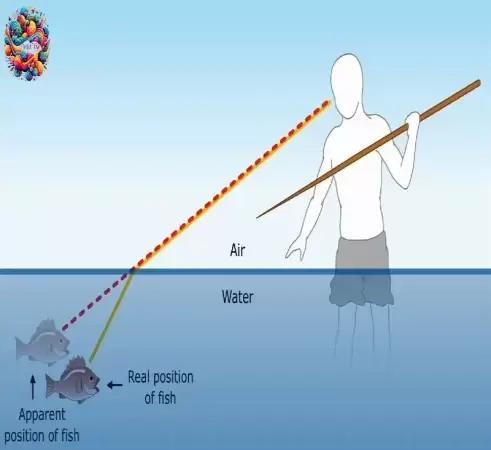
![[Vật lý 7] Nhận biết ánh sáng - Nguồn sáng và vật sáng trong](https://vatly.edu.vn/upload/491x654/2024/07/vat-ly-7-nhan-biet-anh-sang-nguon-sang-va-vat-sang-trong-491x654.webp)