Tìm hiểu quá trình đẳng tích, định luật Sác lơ – Vật lý 10
Định luật Sác lơ là một trong những nguyên lý cơ bản trong vật lý nhiệt động học, mô tả mối quan hệ giữa áp suất và nhiệt độ của một chất khí trong điều kiện thể tích không đổi. Hiểu rõ định luật Sác lơ giúp giải thích và dự đoán chính xác sự biến đổi của các khí lý tưởng trong các thí nghiệm và ứng dụng thực tế, đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và công nghệ.
Quá trình đẳng tích là gì?
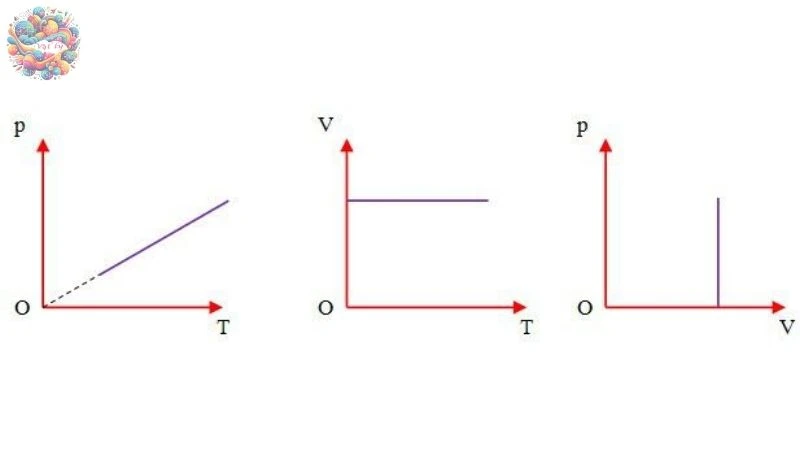
Quá trình đẳng tích là một khái niệm trong nhiệt động học, mô tả sự thay đổi trạng thái của một chất khí khi thể tích của nó được giữ nguyên không đổi. Trong quá trình này, thể tích của khí không thay đổi, dù các yếu tố khác như nhiệt độ và áp suất có thể thay đổi.
Nhiệt độ tuyệt đối được đo bằng thang Kelvin, được đặt tên theo nhà vật lý học người Scotland, William Thomson (Lord Kelvin) (1824–1907). Thang nhiệt độ này sử dụng đơn vị Kelvin (K), trong đó điểm không tuyệt đối (0 K) là mức nhiệt độ thấp nhất có thể đạt được trong tự nhiên. Công thức chuyển đổi từ độ Celsius (độ C) sang Kelvin là:
\[K = C + 273 \quad \text{hoặc} \quad T = t + 273\]
Trong đó:
- \(K\) là nhiệt độ tuyệt đối (đo bằng Kelvin),
- \(t\) là nhiệt độ theo độ Celsius.
Thang Kelvin rất quan trọng trong các tính toán nhiệt động học vì nó bắt đầu từ nhiệt độ thấp nhất có thể, cho phép các nhà khoa học nghiên cứu các hiện tượng vật lý ở những mức năng lượng cực thấp.
Định luật Sác lơ và ứng dụng trong quá trình đẳng tích
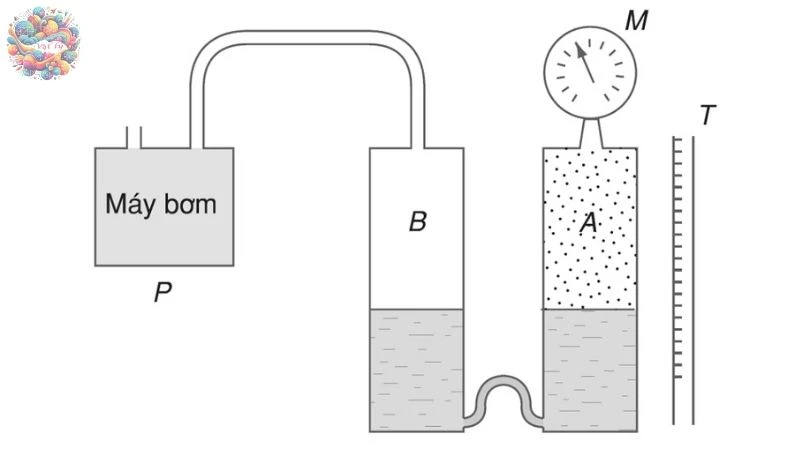
Định luật Sác lơ mô tả mối quan hệ giữa áp suất và nhiệt độ tuyệt đối của một lượng khí lý tưởng khi thể tích được giữ không đổi. Theo định luật này, với một khối lượng khí cố định, khi thể tích không thay đổi, áp suất của khí sẽ thay đổi tỷ lệ thuận với nhiệt độ tuyệt đối của nó. Nói cách khác, khi nhiệt độ tuyệt đối tăng, áp suất cũng tăng và ngược lại, miễn là thể tích vẫn không đổi.
Các công thức của định luật Sác lơ:
Mối quan hệ giữa áp suất (p) và nhiệt độ tuyệt đối (T) trong quá trình đẳng tích được biểu thị bằng công thức:
\[\frac{p_1}{T_1} = \frac{p_2}{T_2} = \ldots = \frac{p_n}{T_n} = \text{hằng số}\]
Trong đó:
- \(p_1\), \(p_2\) là áp suất của khí ở các trạng thái khác nhau (trạng thái 1, trạng thái 2, …),
- \(T_1\), \(T_2\) là nhiệt độ tuyệt đối tương ứng của khí ở các trạng thái đó.
Công thức này cho thấy rằng tỷ số giữa áp suất và nhiệt độ tuyệt đối của một khối khí lý tưởng không đổi nếu thể tích của khối khí đó được giữ nguyên. Điều này có nghĩa là nếu ta biết áp suất và nhiệt độ ở một trạng thái cụ thể, ta có thể tính toán áp suất hoặc nhiệt độ ở một trạng thái khác, miễn là thể tích không thay đổi.
Các bài tập cơ bản về quá trình đẳng tích và định luật Sác lơ
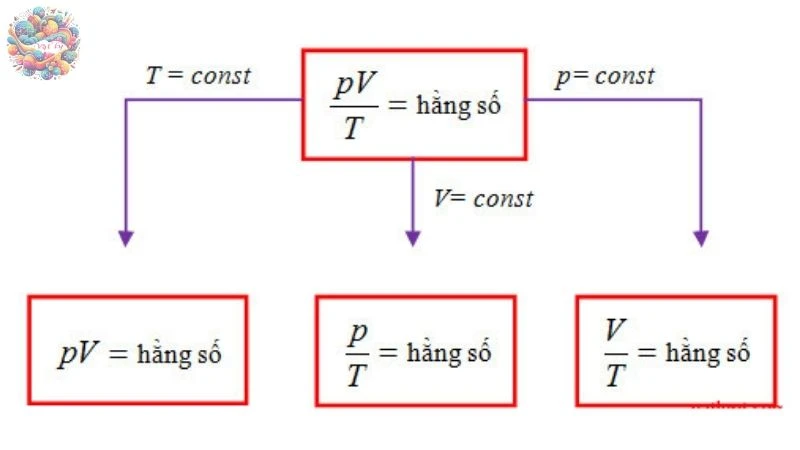
Định luật Sác lơ chỉ ra rằng trong một quá trình đẳng tích (thể tích không đổi), áp suất của một lượng khí lý tưởng tỷ lệ thuận với nhiệt độ tuyệt đối của nó. Công thức thể hiện mối quan hệ này là:
\[\frac{p_1}{T_1} = \frac{p_2}{T_2} = \ldots = \frac{p_n}{T_n}\]
Điều này có nghĩa là áp suất \(p\) của khí sẽ tăng hoặc giảm tương ứng với sự thay đổi của nhiệt độ tuyệt đối \(T\).
Trong đó:
- \(p\): áp suất của khí,
- \(T\): nhiệt độ tuyệt đối (đơn vị Kelvin, K).
Công thức chuyển đổi nhiệt độ từ độ Celsius sang Kelvin là:
\[T(K) = t(°C) + 273\]
Các dạng bài tập về quá trình đẳng tích và định luật Sác lơ:
1. Thay đổi nhiệt độ hoặc áp suất:
– Khi nhiệt độ tăng thêm một lượng \(\Delta T\), nhiệt độ mới sẽ là:
\[T_2 = T_1 + \Delta T\]
– Khi áp suất tăng thêm một lượng \(\Delta p\), áp suất mới sẽ là:
\[p_2 = p_1 + \Delta p\]
– Tương tự, khi nhiệt độ giảm đi một lượng \(\Delta T\), ta có:
\[T_2 = T_1 – \Delta T\]
– Và khi áp suất giảm đi một lượng \(\Delta p\):
\[p_2 = p_1 – \Delta p\]
2. Nhiệt độ hoặc áp suất thay đổi theo tỷ lệ:
– Nếu nhiệt độ giảm đi \(n\) lần, nhiệt độ mới sẽ là:
\[T_2 = \frac{T_1}{n}\]
– Nếu áp suất giảm đi \(n\) lần, áp suất mới sẽ là:
\[p_2 = \frac{p_1}{n}\]
– Nếu nhiệt độ tăng lên \(n\) lần, nhiệt độ mới là:
\[T_2 = n \times T_1\]
– Nếu áp suất tăng lên \(n\) lần, áp suất mới là:
\[p_2 = n \times p_1\]
Bài tập ứng dụng về quá trình đẳng tích và định luật Sác lơ
Bài 1: Một bình kín chứa khí lý tưởng có thể tích không đổi với áp suất ban đầu là \(1.5 \times 10^5\) Pa ở nhiệt độ \(20^\circ\)C. Tính áp suất trong bình khi nhiệt độ tăng lên đến \(40^\circ\)C.
Lời giải:
– Đổi nhiệt độ từ độ Celsius sang Kelvin:
\(T_1 = 20 + 273 = 293\) K
\(T_2 = 40 + 273 = 313\) K
– Tính áp suất \(p_2\):
\[\frac{1.5 \times 10^5}{293} = \frac{p_2}{313}\]
\[p_2 = \frac{1.5 \times 10^5 \times 313}{293} \approx 1.6 \times 10^5 \, \text{Pa}\]
Áp suất trong bình khi nhiệt độ tăng đến \(40^\circ\)C là khoảng \(1.6 \times 10^5\) Pa.
Bài 2: Một bình kín chứa khí có thể tích không đổi ở nhiệt độ ban đầu là \(33^\circ\)C và áp suất ban đầu là \(300\) kPa. Khi nhiệt độ tăng lên đến \(37^\circ\)C, tính độ tăng áp suất trong bình.
Lời giải:
– Đổi nhiệt độ từ độ Celsius sang Kelvin:
\(T_1 = 33 + 273 = 306\) K
\(T_2 = 37 + 273 = 310\) K
– Áp dụng định luật Sác lơ:
\[\frac{300}{306} = \frac{p_2}{310}\]
\[p_2 = \frac{300 \times 310}{306} \approx 304 \, \text{kPa}\]
– Độ tăng áp suất:
\[\Delta p = p_2 – p_1 = 304 – 300 = 4 \, \text{kPa}\]
Độ tăng áp suất khi nhiệt độ tăng từ \(33^\circ\)C đến \(37^\circ\)C là \(4\) kPa.
Bài 3: Một lốp xe chứa không khí ở áp suất \(2\) atm và nhiệt độ \(20^\circ\)C. Lốp xe chịu được áp suất tối đa là \(2.4\) atm. Khi nhiệt độ bên trong lốp xe tăng lên đến \(42^\circ\)C, lốp xe có bị nổ không?
Lời giải:
– Đổi nhiệt độ từ độ Celsius sang Kelvin:
\(T_1 = 20 + 273 = 293\) K
\(T_2 = 42 + 273 = 315\) K
– Áp dụng định luật Sác lơ: \(\frac{p_1}{T_1} = \frac{p_2}{T_2}\)
\[\frac{2}{293} = \frac{p_2}{315}\]
\[p_2 = \frac{2 \times 315}{293} \approx 2.15 \, \text{atm}\]
Áp suất trong lốp xe ở \(42^\circ\)C là khoảng \(2.15\) atm, thấp hơn ngưỡng tối đa \(2.4\) atm, do đó lốp xe không bị nổ.
Bài 4: Một bình thủy tinh có thể tích không đổi chứa không khí ở điều kiện tiêu chuẩn (áp suất \(1\) atm, nhiệt độ \(0^\circ\)C). Tính áp suất khí trong bình khi nhiệt độ tăng lên đến \(200^\circ\)C.
Lời giải:
– Đổi nhiệt độ từ độ Celsius sang Kelvin:
\(T_1 = 0 + 273 = 273\) K
\(T_2 = 200 + 273 = 473\) K
– Áp dụng định luật Sác lơ: \(\frac{p_1}{T_1} = \frac{p_2}{T_2}\)
\[\frac{1}{273} = \frac{p_2}{473}\]
\[p_2 = \frac{473}{273} \approx 1.73 \, \text{atm}\]
Áp suất trong bình sau khi nung nóng lên \(200^\circ\)C là khoảng \(1.73\) atm.
Bài 5: Một bình kín chứa khí lý tưởng có thể tích không đổi ở nhiệt độ \(27^\circ\)C và áp suất ban đầu là \(1\) atm. Biết rằng áp suất sau khi tăng nhiệt độ là \(2.5\) atm, tính nhiệt độ tăng thêm trong bình.
Lời giải:
– Đổi nhiệt độ từ độ Celsius sang Kelvin:
\(T_1 = 27 + 273 = 300\) K
– Áp dụng định luật Sác lơ: \(\frac{p_1}{T_1} = \frac{p_2}{T_2}\)
\[\frac{1}{300} = \frac{2.5}{T_2}\]
\[T_2 = \frac{2.5 \times 300}{1} = 750 \, \text{K}\]
– Đổi nhiệt độ từ Kelvin sang độ Celsius:
\(T_2 = 750 – 273 = 477^\circ\)C
– Độ tăng nhiệt độ:
\[\Delta T = 477 – 27 = 450^\circ\text{C}\]
Nhiệt độ trong bình tăng thêm \(450^\circ\)C để áp suất tăng từ \(1\) atm lên \(2.5\) atm.
Bài 6: Một bóng đèn dây tóc chưa phát sáng chứa khí lý tưởng ở nhiệt độ ban đầu \(27^\circ\)C. Khi bóng đèn phát sáng, nhiệt độ tăng lên \(105^\circ\)C, và áp suất trong bóng đèn tăng thêm \(0.2\) atm. Hãy tính áp suất bên trong bóng đèn trước khi phát sáng.
Lời giải:
– Đổi nhiệt độ từ độ Celsius sang Kelvin:
\[T_1 = 27 + 273 = 300 \, \text{K}\]
\[T_2 = 105 + 273 = 378 \, \text{K}\]
– Gọi \(p_1\) là áp suất ban đầu và \(p_2 = p_1 + 0.2\) là áp suất sau khi nhiệt độ tăng.
– Áp dụng định luật Sác lơ:
\[\frac{p_1}{T_1} = \frac{p_2}{T_2}\]
\[\frac{p_1}{300} = \frac{p_1 + 0.2}{378}\]
– Giải phương trình để tìm \(p_1\):
\[p_1 \times 378 = (p_1 + 0.2) \times 300\]
\[378p_1 = 300p_1 + 60\]
\[78p_1 = 60\]
\[p_1 = \frac{60}{78} \approx 0.769 \, \text{atm}\]
Áp suất bên trong bóng đèn trước khi phát sáng là khoảng \(0.769\) atm.
Bài 7: Một khối khí lý tưởng tăng áp suất lên ba lần trong khi giữ thể tích không đổi, và nhiệt độ tăng thêm \(600\) K. Tính nhiệt độ ban đầu của khối khí.
Lời giải:
– Gọi \(T_1\) là nhiệt độ ban đầu và \(T_2 = T_1 + 600\) là nhiệt độ sau khi tăng.
– Áp suất tăng lên ba lần, do đó, \(\frac{p_2}{p_1} = 3\).
– Áp dụng định luật Sác lơ:
\[\frac{p_1}{T_1} = \frac{p_2}{T_2} \implies \frac{p_1}{T_1} = \frac{3p_1}{T_2}\]
\[\frac{1}{T_1} = \frac{3}{T_1 + 600}\]
\[T_1 + 600 = 3T_1\]
\[600 = 2T_1\]
\[T_1 = 300 \, \text{K}\]
Nhiệt độ ban đầu của khối khí là \(300\) K.
Bài 8: Một bóng đèn chứa khí trơ có nhiệt độ \(25^\circ\)C khi tắt và \(323^\circ\)C khi sáng. Hỏi áp suất của khí trong bóng đèn tăng bao nhiêu lần khi đèn phát sáng?
Lời giải:
– Đổi nhiệt độ từ độ Celsius sang Kelvin:
\[T_1 = 25 + 273 = 298 \, \text{K}\]
\[T_2 = 323 + 273 = 596 \, \text{K}\]
– Tỷ lệ tăng áp suất được xác định bởi:
\[\frac{p_2}{p_1} = \frac{T_2}{T_1} = \frac{596}{298} \approx 2\]
Áp suất khí trơ trong bóng đèn tăng lên gấp đôi khi đèn phát sáng.
Bài 9: Khi đun nóng đẳng tích một khối khí, nhiệt độ tăng thêm \(1\) K và áp suất tăng thêm \(\frac{1}{360}\) lần so với áp suất ban đầu. Tính nhiệt độ ban đầu của khối khí.
Lời giải:
– Gọi \(T_1\) là nhiệt độ ban đầu (K), \(T_2 = T_1 + 1\).
– Áp suất tăng thêm \(\frac{1}{360} p_1\), nên \(p_2 = p_1 + \frac{p_1}{360}\).
– Áp dụng định luật Sác lơ:
\[\frac{p_1}{T_1} = \frac{p_2}{T_2}\]
\[\frac{p_1}{T_1} = \frac{p_1 + \frac{p_1}{360}}{T_1 + 1}\]
\[\frac{1}{T_1} = \frac{1 + \frac{1}{360}}{T_1 + 1}\]
\[T_1 + 1 = \frac{T_1}{1 + \frac{1}{360}}\]
\[T_1 + 1 = \frac{360T_1}{361}\]
\[361(T_1 + 1) = 360T_1\]
\[361T_1 + 361 = 360T_1\]
\[T_1 = 361 \, \text{K}\]
Nhiệt độ ban đầu của khối khí là \(361\) K.
Bài 10: Một bình kín chứa không khí ở điều kiện tiêu chuẩn và được đậy bằng một nắp có khối lượng \(m = 2\) kg. Diện tích miệng bình là \(10 \, \text{cm}^2\). Tìm nhiệt độ cực đại của không khí trong bình để nắp không bị đẩy lên, biết áp suất khí quyển là \(p_0 = 1\) atm.
Lời giải:
– Lực do áp suất khí tác động lên nắp: \(F = p \cdot A\)
– Áp lực do khối lượng của nắp: \(F = mg\), với \(g = 9.8 \, \text{m/s}^2\)
– Diện tích \(A = 10 \, \text{cm}^2 = 10^{-3} \, \text{m}^2\)
– Áp suất cực đại bên trong bình \(p = p_0 + \frac{mg}{A}\)
\[p = 1 + \frac{2 \times 9.8}{10^{-3}} \times \frac{1}{101325} \approx 1.0019 \, \text{atm}\]
– Áp dụng định luật Sác lơ: \(\frac{p_1}{T_1} = \frac{p_2}{T_2}\)
\[T_1 = 273 \, \text{K} \quad (điều kiện tiêu chuẩn)\]
\[\frac{1}{273} = \frac{1.0019}{T_2}\]
\[T_2 = 273 \times 1.0019 \approx 273.52 \, \text{K}\]
Nhiệt độ cực đại của không khí trong bình để nắp không bị đẩy lên là khoảng \(273.52\) K, tức xấp xỉ \(0.52^\circ\)C.
Việc hiểu rõ định luật Sác lơ là chìa khóa để phân tích các hiện tượng liên quan đến khí lý tưởng, từ đó ứng dụng vào thực tế trong nhiều lĩnh vực như công nghiệp và khoa học. Định luật này không chỉ giúp giải thích sự thay đổi của áp suất và nhiệt độ mà còn cung cấp nền tảng vững chắc cho việc nghiên cứu và phát triển công nghệ mới. Tìm hiểu thêm về các định luật vật lý quan trọng tại vatly.edu.vn để khám phá thêm nhiều kiến thức thú vị khác.
