Tìm hiểu thuyết động học phân tử chất khí - Vật lý 12
Khám phá thuyết động học phân tử chất khí với các bài giảng dễ hiểu và ví dụ cụ thể. Học cách áp dụng kiến thức này vào bài tập Vật lý và các ứng dụng thực tế.
Thuyết động học phân tử chất khí là một chủ đề quan trọng trong chương trình Vật lý lớp 12, giúp giải thích hành vi của các phân tử khí dựa trên chuyển động và va chạm của chúng. Hiểu rõ thuyết này sẽ cung cấp nền tảng vững chắc để giải các bài tập và áp dụng trong thực tế. Tìm hiểu chi tiết về thuyết động học phân tử chất khí qua các bài giảng và ví dụ minh họa tại đây
Cấu tạo chất
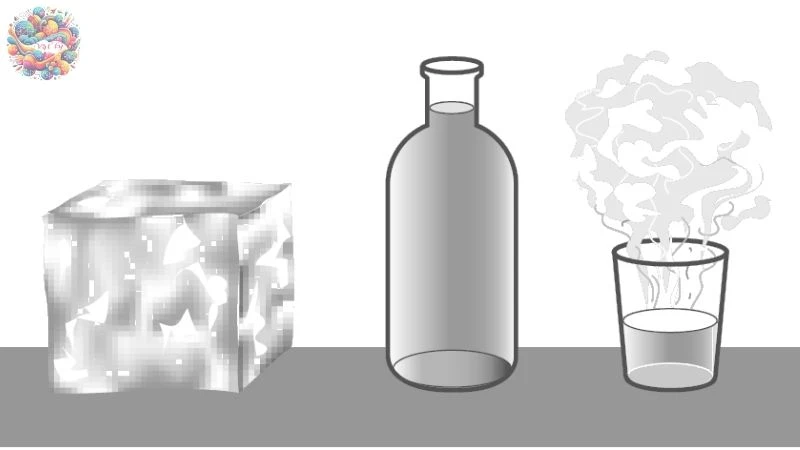
Cấu tạo của chất
- Các chất được hình thành từ những hạt nhỏ riêng biệt, được gọi là các phân tử.
- Các phân tử luôn di chuyển liên tục và không ngừng nghỉ.
- Tốc độ chuyển động của phân tử càng nhanh, nhiệt độ của chất càng tăng.
Lực tương tác giữa các phân tử:
- Giữa các phân tử trong chất luôn tồn tại lực hút và lực đẩy.
- Khi khoảng cách giữa các phân tử nhỏ, lực đẩy sẽ lớn hơn lực hút. Ngược lại, khi khoảng cách giữa các phân tử lớn, lực hút sẽ mạnh hơn lực đẩy. Trong trường hợp khoảng cách giữa các phân tử rất lớn, lực tương tác giữa chúng trở nên không đáng kể.
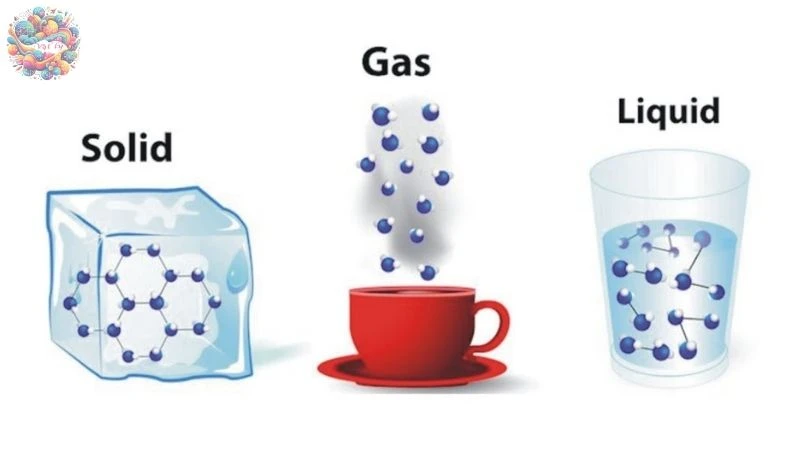
So sánh đặc tính của chất rắn, chất lỏng và chất khí:
| Tính chất | Rắn | Lỏng | Khí |
| Lực tương tác phân tử | Rất mạnh | Lớn hơn chất khí, nhỏ hơn chất rắn | Rất yếu |
| Chuyển động phân tử | Dao động quanh vị trí cân bằng (VTCB) | Dao động quanh VTCB, có thể di chuyển | Hỗn loạn |
| Hình dạng | Xác định | Phụ thuộc bình chứa | Không xác định |
| Thể tích | Xác định | Xác định | Thể tích bình chứa |
Đặc điểm nổi bật của chất khí
- Khả năng bành trướng: Chất khí có khả năng lan tỏa và chiếm toàn bộ thể tích của bình chứa, bất kể kích thước của bình.
- Dễ bị nén: Chất khí rất nhạy cảm với sự thay đổi của áp suất. Khi áp suất tác dụng lên chất khí tăng, thể tích của nó giảm đáng kể.
- Khối lượng riêng nhỏ: So với chất rắn và chất lỏng, khối lượng riêng của chất khí thấp hơn nhiều, khiến chúng nhẹ hơn và dễ di chuyển.
Nguyên lý động học của phân tử trong chất khí
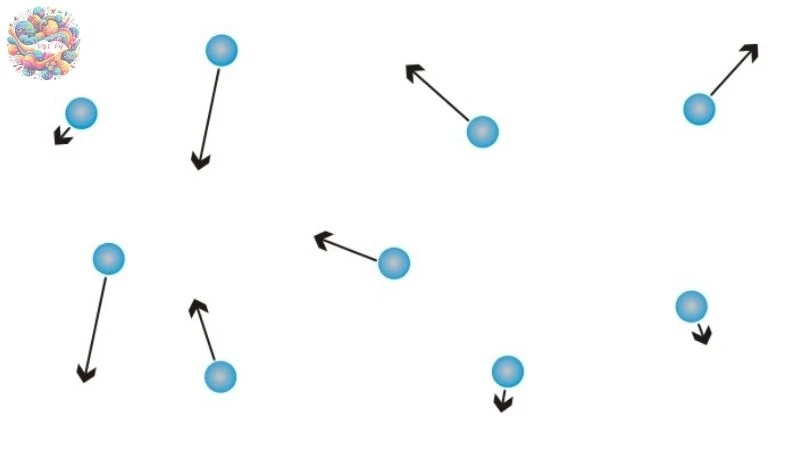
- Cấu tạo của chất khí: Chất khí bao gồm những phân tử nhỏ bé có kích thước rất nhỏ so với khoảng cách giữa chúng, tạo nên một không gian trống rỗng lớn giữa các phân tử.
- Chuyển động hỗn loạn của phân tử khí: Các phân tử trong chất khí luôn chuyển động ngẫu nhiên và không ngừng nghỉ. Tốc độ chuyển động của các phân tử càng lớn, nhiệt độ của chất khí càng cao, biểu hiện cho năng lượng nhiệt trong hệ.
- Tạo áp suất do va chạm: Trong quá trình chuyển động hỗn loạn, các phân tử khí liên tục va chạm với nhau và với thành bình chứa. Những va chạm này tạo ra áp lực lên thành bình, được cảm nhận dưới dạng áp suất của chất khí.
Phân loại và đặc tính của các loại khí
– Khí thực: Đây là các chất khí hiện diện trong đời sống thực tế mà chúng ta thường biết đến như oxy (O₂), nitơ (N₂), carbon dioxide (CO₂), và nhiều loại khí khác. Chúng có các tính chất và hành vi thực tế chịu ảnh hưởng của lực tương tác giữa các phân tử.
– Khí lý tưởng: Đây là mô hình lý thuyết của chất khí, trong đó các phân tử được coi là các chất điểm, không có thể tích và chỉ tương tác khi chúng va chạm. Khí lý tưởng không tồn tại trong thực tế, nhưng là một mô hình hữu ích để đơn giản hóa các tính toán và lý thuyết.
Công thức xác định số mol, thể tích, và khối lượng của chất khí
– Định nghĩa về số mol: Một mol là lượng chất chứa số Avogadro các phân tử hoặc nguyên tử, bằng với số nguyên tử có trong 12 gram cacbon-12 (^12C).
– Số Avogadro (Nₐ): Là số lượng hạt (nguyên tử hoặc phân tử) trong 1 mol chất, được xác định là \(N_A = 6,022 \times 10^{23} \, \text{mol}^{-1}\).
– Số mol của một chất khí (n): Công thức tính số mol được cho bởi:
\[n = \frac{m}{M}\]
Trong đó:
- \(m\) là khối lượng của chất khí (tính bằng gram, g).
- \(M\) là khối lượng mol của phân tử khí (tính bằng gram trên mol, g/mol).
– Số mol ở điều kiện tiêu chuẩn (đktc):Khi khí được đo ở điều kiện tiêu chuẩn (áp suất 1 atm, nhiệt độ 0°C), số mol có thể được tính theo thể tích như sau:
\[n = \frac{V}{22,4}\]
Trong đó:
- \(V\) là thể tích của khí (tính bằng lít, l).
- Số phân tử hoặc nguyên tử (N): Số phân tử trong một khối lượng \(m\) của chất có thể được tính bằng:
\[N = n \times N_A = \frac{m}{M} \times N_A\]
- Mật độ phân tử của chất khí: Mật độ phân tử (số phân tử trong một đơn vị thể tích) có thể được tính theo công thức:
\[n’ = \frac{N}{V}\]
Bài tập ứng dụng về thuyết động học phân tử chất khí

Bài tập 1: Một bình kín chứa 0,5 mol khí lý tưởng ở nhiệt độ 27°C. Thể tích của bình là 10 lít. Hãy tính áp suất của khí trong bình.
Gợi ý lời giải:
1. Chuyển đổi đơn vị nhiệt độ: Nhiệt độ cần được chuyển sang độ Kelvin:
\[T = 27 + 273 = 300 \, \text{K}\]
2. Sử dụng phương trình trạng thái khí lý tưởng:
Phương trình trạng thái khí lý tưởng là:
\[PV = nRT\]
Trong đó:
- \(P\) là áp suất của khí.
- \(V = 10\) lít = \(0.01\) m³ (chuyển đổi từ lít sang mét khối).
- \(n = 0.5\) mol.
- \(R = 8.314 \, \text{J/(mol·K)}\) là hằng số khí lý tưởng.
- \(T = 300 \, \text{K}\).
3. Tính áp suất \(P\):
\[P = \frac{nRT}{V} = \frac{0.5 \times 8.314 \times 300}{0.01}\]
\[P = \frac{1247.1}{0.01} = 124710 \, \text{Pa}\]
=> Kết quả: Áp suất của khí trong bình là \(124710\) Pa (khoảng \(124.7\) kPa).
Bài tập 2: Tính tốc độ trung bình của các phân tử khí ôxi (O₂) ở 0°C. Biết khối lượng mol của O₂ là 32 g/mol.
Gợi ý lời giải:
1. Chuyển đổi đơn vị nhiệt độ:
\[T = 0 + 273 = 273 \, \text{K}\]
2. Tính khối lượng phân tử của O₂:
Khối lượng phân tử của O₂:
\[m = \frac{32 \times 10^{-3}}{6.022 \times 10^{23}} \, \text{kg}\]
3. Sử dụng công thức tính tốc độ trung bình:
Công thức tính tốc độ trung bình \(v\) của phân tử khí là:
\[v = \sqrt{\frac{8RT}{\pi m}}\]
Thay số vào công thức:
\[v = \sqrt{\frac{8 \times 8.314 \times 273}{\pi \times \frac{32 \times 10^{-3}}{6.022 \times 10^{23}}}}\]
4. Tính toán:
\[m = \frac{32 \times 10^{-3}}{6.022 \times 10^{23}} = 5.32 \times 10^{-26} \, \text{kg}\]
\[v = \sqrt{\frac{8 \times 8.314 \times 273}{\pi \times 5.32 \times 10^{-26}}}\]
\[v \approx 395 \, \text{m/s}\]
=> Kết quả: Tốc độ trung bình của phân tử O₂ ở 0°C là khoảng \(395 \, \text{m/s}\).

Bài tập 3: Tính năng lượng động học trung bình của các phân tử khí nitơ (N₂) ở nhiệt độ 27°C.
Gợi ý lời giải:
1. Chuyển đổi nhiệt độ sang độ Kelvin:
\[T = 27 + 273 = 300 \, \text{K}\]
2. Sử dụng công thức năng lượng động học trung bình:
Công thức tính năng lượng động học trung bình của một phân tử khí là:
\[\bar{E} = \frac{3}{2} kT\]
Trong đó:
– \(k = 1.38 \times 10^{-23} \, \text{J/K}\) là hằng số Boltzmann.
3. Tính toán:
\[\bar{E} = \frac{3}{2} \times 1.38 \times 10^{-23} \times 300\]
\[\bar{E} = 6.21 \times 10^{-21} \, \text{J}\]
=> Kết quả: Năng lượng động học trung bình của các phân tử khí nitơ ở 27°C là \(6.21 \times 10^{-21} \, \text{J}\).
Bài tập 4: Một bình chứa 1 mol khí lý tưởng ở nhiệt độ 300K và thể tích 22,4 lít. Tính số phân tử va chạm vào thành bình trong 1 giây, biết diện tích thành bình là 1 m².
Gợi ý lời giải:
1. Tính số phân tử:
\[N = n \times N_A = 1 \times 6.022 \times 10^{23} = 6.022 \times 10^{23}\]
2. Tính tốc độ trung bình:
Công thức tốc độ trung bình \(v_{tb}\) cho khí lý tưởng:
\[v_{tb} = \sqrt{\frac{8RT}{\pi M}}\]
Trong đó \(M = 0.032 \, \text{kg/mol}\) (khối lượng mol của khí).
\[v_{tb} = \sqrt{\frac{8 \times 8.314 \times 300}{\pi \times 0.032}}\]
\[v_{tb} \approx 395 \, \text{m/s}\]
3. Tính số phân tử va chạm vào thành bình:
Số phân tử va chạm vào thành bình trong 1 giây:
\[Z = \frac{N \times v_{tb}}{4V} \times A\]
\[Z = \frac{6.022 \times 10^{23} \times 395}{4 \times 0.0224} \times 1\]
\[Z \approx 2.66 \times 10^{25}\]
=> Kết quả: Số phân tử va chạm vào thành bình trong 1 giây là khoảng \(2.66 \times 10^{25}\) phân tử.

Bài tập 5: Một khí lý tưởng chứa trong một bình kín có thể tích không đổi. Nếu nhiệt độ của khí tăng từ 27°C lên 127°C thì nhiệt lượng truyền cho khí là bao nhiêu? Biết số mol khí là 2 mol và dung lượng nhiệt đẳng tích của khí là \(C_V = \frac{5}{2} R\).
Gợi ý lời giải:
1. Chuyển đổi nhiệt độ:
\[T_1 = 27 + 273 = 300 \, \text{K}, \quad T_2 = 127 + 273 = 400 \, \text{K}\]
2. Tính nhiệt lượng truyền cho khí:
Công thức tính nhiệt lượng truyền cho khí:
\[Q = n C_V \Delta T\]
Trong đó:
- \(\Delta T = T_2 – T_1 = 400 – 300 = 100 \, \text{K}\),
- \(C_V = \frac{5}{2} R = \frac{5}{2} \times 8.314 = 20.785 \, \text{J/(mol·K)}\).
\[Q = 2 \times 20.785 \times 100\]
\[Q = 4157 \, \text{J}\]
=> Kết quả: Nhiệt lượng truyền cho khí là \(4157 \, \text{J}\).
Bài tập 6: Một khinh khí cầu chứa 10 m³ khí heli (He) ở nhiệt độ 20°C và áp suất 1 atm. Khi bay lên cao, nhiệt độ bên trong khinh khí cầu không đổi, nhưng áp suất giảm theo độ cao. Tính độ cao tối đa mà khinh khí cầu có thể đạt được nếu áp suất giảm xuống còn 0.2 atm. Biết khối lượng mol của He là 4 g/mol và bỏ qua sự thay đổi của trọng lực theo độ cao.
Gợi ý lời giải:
1. Chuyển đổi nhiệt độ sang độ Kelvin:
\[T = 20 + 273 = 293 \, \text{K}\]
2. Sử dụng phương trình trạng thái khí lý tưởng cho áp suất ban đầu và áp suất ở độ cao h:
Phương trình trạng thái khí lý tưởng:
\[P_1 V = nRT \quad \text{và} \quad P_2 V = nRT\]
Suy ra:
\[\frac{P_1}{P_2} = \frac{nRT}{nRT} = \frac{P_1}{P_2} \Rightarrow P_1V = P_2V\]
3. Tính số mol khí heli:
\[n = \frac{P_1 V}{RT} = \frac{1 \times 10}{8.314 \times 293}\]
\[n \approx 0.412 \, \text{mol}\]
4. Áp dụng công thức áp suất và độ cao:
Sử dụng công thức áp suất giảm theo độ cao:
\[P_2 = P_1 e^{-\frac{Mgh}{RT}}\]
Trong đó:
- \(M = 4 \times 10^{-3} \, \text{kg/mol}\) là khối lượng mol của khí heli.
- \(g = 9.8 \, \text{m/s}^2\) là gia tốc trọng trường.
- \(h\) là độ cao cần tìm.
5. Giải phương trình cho \(h\):
\[0.2 = 1 \times e^{-\frac{4 \times 10^{-3} \times 9.8 \times h}{8.314 \times 293}}\]
\[\ln(0.2) = -\frac{0.0392h}{8.314 \times 293}\]
\[h = -\frac{\ln(0.2) \times 8.314 \times 293}{0.0392}\]
\[h \approx 16600 \, \text{m}\]
=> Kết quả: Độ cao tối đa mà khinh khí cầu có thể đạt được là khoảng 16.600 m.

Bài tập 7: Tính tốc độ thoát (escape velocity) của các phân tử khí hydro (H₂) từ bề mặt Trái Đất. Biết khối lượng mol của H₂ là 2 g/mol, và gia tốc trọng trường \(g = 9.8 \, \text{m/s}^2\).
Gợi ý lời giải:
1. Công thức tính tốc độ thoát:
Tốc độ thoát \(v_e\) từ bề mặt Trái Đất được tính bằng:
\[v_e = \sqrt{\frac{2GM}{R}}\]
Trong đó:
- \(G = 6.67 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2\) là hằng số hấp dẫn.
- \(M = 5.97 \times 10^{24} \, \text{kg}\) là khối lượng Trái Đất.
- \(R = 6.37 \times 10^6 \, \text{m}\) là bán kính Trái Đất.
2. Tính tốc độ thoát:
\[v_e = \sqrt{\frac{2 \times 6.67 \times 10^{-11} \times 5.97 \times 10^{24}}{6.37 \times 10^6}}\]
\[v_e \approx 11186 \, \text{m/s}\]
=> Kết quả: Tốc độ thoát của phân tử khí hydro từ bề mặt Trái Đất là khoảng \(11186 \, \text{m/s}\).
Bài tập 8: Một mẫu khí lý tưởng ở nhiệt độ 300 K, có các phân tử khí có mức năng lượng phân bố theo định luật phân bố Maxwell-Boltzmann. Tính tỉ lệ số phân tử có năng lượng lớn hơn gấp 3 lần năng lượng động học trung bình so với tổng số phân tử.
Gợi ý lời giải:
1. Công thức năng lượng động học trung bình:
\[\bar{E} = \frac{3}{2} kT\]
Trong đó:
- \(k = 1.38 \times 10^{-23} \, \text{J/K}\) là hằng số Boltzmann,
- \(T = 300 \, \text{K}\).
2. Năng lượng \(E\) lớn hơn 3 lần năng lượng động học trung bình:
\[E = 3\bar{E} = 3 \times \frac{3}{2} kT = \frac{9}{2} kT\]
3. Xác suất phân tử có năng lượng \(E > \frac{9}{2} kT\):
Xác suất được tính theo phân bố Maxwell-Boltzmann:
\[f(E) = \left( \frac{E}{kT} \right)^{3/2} e^{-E/kT}\]
Xác suất để \(E > \frac{9}{2} kT\) có thể tính bằng tích phân từ \(E = \frac{9}{2} kT\) đến vô cực. Tuy nhiên, ta có thể sử dụng bảng phân bố chuẩn hóa hoặc hàm lũy tích để tìm tỉ lệ này. Theo tính toán, tỉ lệ số phân tử này sẽ là rất nhỏ, do hàm mũ giảm nhanh.
4. Tỉ lệ xấp xỉ:
\[\text{Tỉ lệ} \approx e^{-9/2} \approx 0.0111\]
=> Kết quả: Tỉ lệ số phân tử có năng lượng lớn hơn 3 lần năng lượng động học trung bình so với tổng số phân tử là khoảng \(1.11\%\).

Bài tập 9: Trong một bình kín có chứa hỗn hợp khí H₂ và O₂ ở nhiệt độ 298 K và áp suất 1 atm. Tính xác suất để xảy ra một phản ứng giữa hai phân tử H₂ và O₂ nếu năng lượng cần thiết để phản ứng xảy ra là 200 kJ/mol.
Gợi ý lời giải:
1. Tính năng lượng cần thiết cho một phản ứng:
\[E_{phản ứng} = \frac{200 \times 10^3}{N_A} \, \text{J}\]
Với \(N_A = 6.022 \times 10^{23} \, \text{mol}^{-1}\):
\[E_{phản ứng} \approx 3.32 \times 10^{-19} \, \text{J}\]
2. Xác suất xảy ra phản ứng:
Xác suất để hai phân tử có năng lượng đủ để xảy ra phản ứng được tính bằng:
\[P(E > E_{phản ứng}) = e^{-E_{phản ứng}/kT}\]
\[P(E > E_{phản ứng}) = e^{-3.32 \times 10^{-19} / (1.38 \times 10^{-23} \times 298)}\]
\[P(E > E_{phản ứng}) \approx e^{-8.04}\]
\[P(E > E_{phản ứng}) \approx 0.00032\]
=> Kết quả: Xác suất để xảy ra một phản ứng giữa hai phân tử H₂ và O₂ là khoảng \(0.032\%\).
Bài tập 10: Một bình kín chứa 2 mol khí lý tưởng ở nhiệt độ 300 K và áp suất 2 atm. Sau đó, nhiệt độ tăng lên 450 K và thể tích của bình giảm đi một nửa. Tính áp suất mới của khí trong bình.
Gợi ý lời giải:
1. Phương trình trạng thái khí lý tưởng ban đầu:
\[P_1V_1 = nRT_1\]
Trong đó \(P_1 = 2 \, \text{atm}, \, T_1 = 300 \, \text{K}\).
2. Phương trình trạng thái khí lý tưởng sau khi thay đổi nhiệt độ và thể tích:
\[P_2V_2 = nRT_2\]
Trong đó:
- \(T_2 = 450 \, \text{K}\),
- \(V_2 = \frac{V_1}{2}\).
3. Tính áp suất mới \(P_2\):
\[\frac{P_2}{P_1} = \frac{T_2}{T_1} \times \frac{V_1}{V_2}\]
\[\frac{P_2}{2} = \frac{450}{300} \times 2\]
\[P_2 = 2 \times \frac{3}{2} \times 2 = 6 \, \text{atm}\]
=> Kết quả: Áp suất mới của khí trong bình là \(6 \, \text{atm}\).
Thuyết động học phân tử chất khí không chỉ mang lại cái nhìn sâu sắc về cấu trúc và tính chất của khí, mà còn mở rộng hiểu biết về cách các nguyên tử và phân tử tương tác trong môi trường thực tế. Nắm vững thuyết này giúp nâng cao khả năng giải quyết vấn đề và ứng dụng kiến thức Vật lý vào cuộc sống. Khám phá thêm nhiều kiến thức thú vị về thuyết động học phân tử chất khí tại vatly.edu.vn.
Bài Viết Liên Quan
Tôi là Kiều Anh, đam mê khám phá và chia sẻ những kiến thức vật lý thú vị từ cuộc sống hằng ngày đến bài học trên lớp. Với cách viết sinh động và dễ hiểu, tôi mong muốn giúp độc giả thấy được vẻ đẹp của vật lý trong mọi khía cạnh của cuộc sống. Hy vọng những bài viết của tôi trên vatly.edu.vn sẽ truyền cảm hứng và làm giàu thêm kiến thức cho mọi người.