Khái niệm về định luật bảo toàn động lượng – Vật Lý 10

Định luật bảo toàn động lượng là một trong những nguyên lý cơ bản và quan trọng nhất trong vật lý. Nó giải thích tại sao các vật thể tương tác với nhau lại có những biến đổi về vận tốc theo những cách nhất định. Cùng vatly.edu.vn khám phá những bí ẩn thú vị của định luật bảo toàn động lượng qua các ví dụ minh họa sinh động và các bài tập thực hành.

Lý thuyết về động lượng 

Xung lượng của lực

– Khi một lực \(\vec{F}\) tác dụng lên một vật trong khoảng thời gian \(\Delta t\), tích số của lực \(\vec{F}\) và khoảng thời gian \(\Delta t\) được gọi là xung lượng của lực trong khoảng thời gian đó. Cụ thể, xung lượng của lực \(\vec{F}\) trong khoảng thời gian \(\Delta t\) được tính theo công thức: 

\[\text{Xung lượng} = \vec{F} \cdot \Delta t\]

– Đơn vị đo lường của xung lượng lực là Newton giây (N.s).

Động lượng

– Động lượng của một vật có khối lượng \(m\) và đang chuyển động với vận tốc \(\vec{v}\) được xác định theo công thức: 

\[\vec{p} = m \cdot \vec{v}\]

Trong đó, \(\vec{p}\) là động lượng.

• Động lượng là một đại lượng vectơ có cùng hướng với vận tốc của vật.
• Đơn vị của động lượng là kilôgam mét trên giây (kg.m/s).

– Sự thay đổi động lượng của một vật trong một khoảng thời gian nhất định sẽ bằng xung lượng của lực tác dụng lên vật trong khoảng thời gian đó. Công thức thể hiện mối quan hệ này là:

\[\Delta \vec{p} = \vec{F} \cdot \Delta t\]

Định luật bảo toàn động lượng 

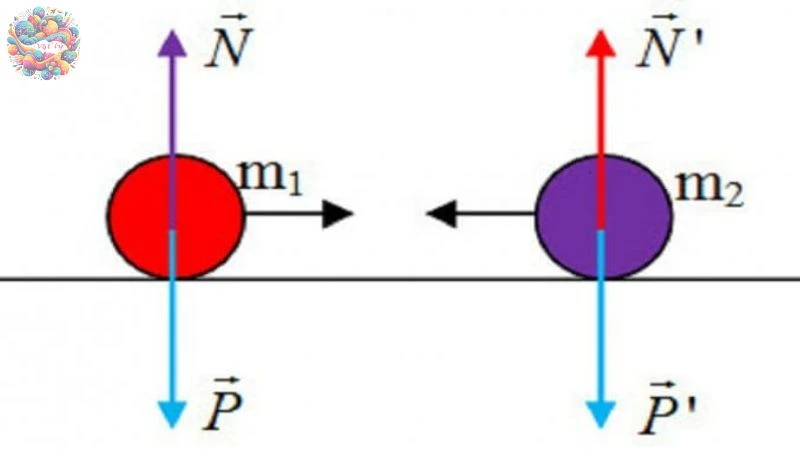
Hệ cô lập

Một hệ gồm nhiều vật được coi là cô lập khi không có bất kỳ ngoại lực nào tác động lên hệ. Nếu có ngoại lực tác động, thì các ngoại lực này phải triệt tiêu lẫn nhau, nghĩa là tổng các ngoại lực bằng không.

Định luật bảo toàn động lượng trong hệ cô lập

Trong một hệ cô lập, động lượng tổng của hệ là một đại lượng không thay đổi theo thời gian. Điều này có nghĩa là tổng động lượng của tất cả các vật trong hệ sẽ được bảo toàn, không bị ảnh hưởng bởi bất kỳ yếu tố bên ngoài nào.

Va chạm mềm

Áp dụng định luật bảo toàn động lượng trong trường hợp va chạm mềm, ta có công thức:

\[m_1 \vec{v}_1 = (m_1 + m_2) \vec{v}\]

Trong đó, \(\vec{v}_1\) là vận tốc của vật có khối lượng \(m_1\) ngay trước khi va chạm với vật có khối lượng \(m_2\) đang đứng yên, và \(\vec{v}\) là vận tốc chung của cả hai vật ngay sau va chạm.

Chuyển động bằng phản lực

Theo định luật bảo toàn động lượng, chuyển động bằng phản lực có thể được mô tả bằng phương trình:

\[m \vec{v} + M \vec{v’} = \vec{0}\]

Trong đó, \(\vec{v}\) là vận tốc của lượng khí có khối lượng \(m\) bị phụt ra phía sau, và \(\vec{v’}\) là vận tốc của tên lửa có khối lượng \(M\) di chuyển về phía trước.

Bài tập ứng dụng về định luật bảo toàn động lượng

Câu hỏi trắc nghiệm

Câu 1. Động lượng của một vật có độ lớn bằng:

A. Tích của khối lượng và vận tốc.

B. Thương của khối lượng và vận tốc.

C. Tích của lực và thời gian tác dụng.

D. Thương của lực và thời gian tác dụng.

Đáp án: A. Tích của khối lượng và vận tốc.

Câu 2. Đơn vị của động lượng là:

A. N/s

B. N.s

C. kg.m/s

D. kg.m/s²

Đáp án: C. kg.m/s

Câu 3. Định luật bảo toàn động lượng phát biểu rằng:

A. Động lượng của một vật không đổi theo thời gian.

B. Tổng động lượng của một hệ kín là một hằng số.

C. Động lượng của hệ kín tăng dần theo thời gian.

D. Động lượng của hệ kín giảm dần theo thời gian.

Đáp án: B. Tổng động lượng của một hệ kín là một hằng số.

Câu 4. Hệ kín là hệ:

A. Chỉ chịu tác dụng của các lực trong hệ.

B. Chỉ chịu tác dụng của các lực ngoài hệ.

C. Không chịu tác dụng của lực nào.

D. Chỉ chịu tác dụng của lực ma sát.

Đáp án: A. Chỉ chịu tác dụng của các lực trong hệ.

Câu 5. Trong va chạm mềm, đại lượng nào sau đây được bảo toàn:

A. Động năng

B. Động lượng

C. Vận tốc

D. Cả A, B, C đều sai

Đáp án: B. Động lượng

Câu 6. Trong va chạm đàn hồi, đại lượng nào sau đây được bảo toàn:

A. Chỉ động năng

B. Chỉ động lượng

C. Cả động năng và động lượng

D. Không có đại lượng nào được bảo toàn

Đáp án: C. Cả động năng và động lượng

Câu 7. Một vật có khối lượng m1 = 2kg đang chuyển động với vận tốc v1 = 3m/s. Nó va chạm vào một vật có khối lượng m2 = 1kg đang đứng yên. Sau va chạm, hai vật dính vào nhau và cùng chuyển động với vận tốc v2 là:

A. 1 m/s

B. 2 m/s

C. 3 m/s

D. 4 m/s

Đáp án: A. 1 m/s

Câu 8. Một quả bóng khối lượng m đang bay với vận tốc v đến đập vuông góc vào một bức tường rồi bật trở lại theo phương cũ với cùng vận tốc. Độ biến thiên động lượng của quả bóng là:

A. 0

B. mv

C. 2mv

D. -2mv

Đáp án: C. 2mv

Câu 9. Một khẩu súng có khối lượng M bắn một viên đạn có khối lượng m. Vận tốc của đạn lúc rời khỏi nòng súng là v. Vận tốc giật lùi của súng là:

A. mv/M

B. Mv/m

C. -mv/M

D. -Mv/m

Đáp án: C. -mv/M

Câu 10. Trong quá trình nào sau đây, động lượng của hệ không bảo toàn:

A. Hai viên bi va chạm nhau.

B. Một quả bóng rơi tự do.

C. Một tên lửa đang hoạt động.

D. Hai vật có khối lượng bằng nhau chuyển động ngược chiều nhau với cùng vận tốc rồi va chạm vào nhau.

Đáp án: C. Một tên lửa đang hoạt động.

Bài tập tự luận

Bài tập 1: Một chiếc xe có khối lượng \(m = 1.5\) tấn đang di chuyển với vận tốc \(54\) km/h thì hãm phanh và dừng lại sau \(6\) giây. Hãy tìm lực hãm tác dụng lên xe, sử dụng hai phương pháp khác nhau dựa trên định luật II Newton.

Lời giải chi tiết

– Chọn vật khảo sát: Xe, với chiều dương là chiều chuyển động ban đầu của xe.

Cách 1: Áp dụng định luật II Newton với khối lượng không đổi

Định luật II Newton khi khối lượng vật không đổi được biểu diễn dưới dạng: 

\[a = \frac{F}{m}\]

– Chuyển đổi vận tốc từ km/h sang m/s:

\[v = 54 \, \text{km/h} = 15 \, \text{m/s}\]

– Tính gia tốc (a):** Gia tốc của xe khi dừng lại có thể tính bằng công thức:

\[a = \frac{\Delta v}{\Delta t} = \frac{0 – 15}{6} = -2.5 \, \text{m/s}^2\]

– Tính lực hãm (F):

\[F = ma = 1500 \times (-2.5) = -3750 \, \text{N}\]

Lực hãm có giá trị là \(3750\) N và ngược hướng với chiều chuyển động ban đầu của xe.

Cách 2: Áp Dụng định luật II Newton dưới dạng tổng quát

– Tính độ biến thiên động lượng (Δp):

Độ biến thiên động lượng được tính bằng công thức:

\[\Delta p = m \Delta v = 1500 \times (0 – 15) = -22500 \, \text{kg.m/s}\]

– Tính lực hãm (F):** Dựa vào định luật II Newton dạng tổng quát:

\[F = \frac{\Delta p}{\Delta t} = \frac{-22500}{6} = -3750 \, \text{N}\]

Lực hãm cũng có giá trị \(3750\) N và ngược chiều với hướng chuyển động của xe.

=> Kết luận: Lực hãm tác dụng lên xe có độ lớn là \(3750\) N và ngược hướng với chiều chuyển động ban đầu của xe.

Bài tập 2: Hãy xác định lực tác dụng của súng trường lên vai người bắn. Biết rằng sau khi bắn, vai người bắn giật lùi 3 cm, viên đạn rời nòng súng với vận tốc 600 m/s. Khối lượng của súng là 4 kg và khối lượng của viên đạn là 30 g.

Lời giải chi tiết:

Chọn hệ khảo sát: Súng và viên đạn.

– Phân tích quá trình giật lùi của súng:

Quá trình giật lùi của súng sau khi bắn viên đạn được chia thành hai giai đoạn:

• Giai đoạn 1: Viên đạn đang chuyển động trong nòng súng.
• Giai đoạn 2: Viên đạn đã ra khỏi nòng súng.

– Do viên đạn rời nòng súng gần như tức thì, chúng ta có thể bỏ qua giai đoạn 1 và chỉ xét giai đoạn 2, khi viên đạn đã rời khỏi nòng súng. Theo định luật bảo toàn động lượng, khi đạn rời khỏi nòng súng với vận tốc \(v_0\), súng sẽ giật lùi với vận tốc \(v\).

Gọi \(m\) là khối lượng của viên đạn và \(M\) là khối lượng của súng, ta có phương trình bảo toàn động lượng:

\[Mv = mv_0\]

Từ đó, vận tốc giật lùi của súng là:

\[v = \frac{mv_0}{M} = \frac{0.03 \times 600}{4} = 4.5 \, \text{m/s}\]

– Chuyển động của súng sau khi viên đạn đã ra khỏi nòng:

Súng sẽ chuyển động chậm dần đều với vận tốc ban đầu \(v = 4.5\) m/s và đi được quãng đường \(s = 0.03\) m trước khi dừng lại do tác dụng của lực cản \(F\) từ vai người bắn.

Theo định lý động năng, công của lực cản \(F\) sẽ bằng độ giảm động năng của súng:

\[A = \frac{1}{2} M v^2 = \frac{1}{2} \times 4 \times (4.5)^2 = 40.5 \, \text{J}\]

Lực cản \(F\) được tính bằng công của lực chia cho quãng đường:

\[F = \frac{A}{s} = \frac{40.5}{0.03} = 1350 \, \text{N}\]

=> Kết luận: Lực tác dụng của súng lên vai người bắn, về độ lớn, bằng với lực cản \(F = 1350\) N và có hướng ngược lại.

Bài tập 3: Một tên lửa có khối lượng ban đầu là 600 kg đang di chuyển với vận tốc 300 m/s. Sau đó, tên lửa tách thành hai phần. Phần tách rời có khối lượng 250 kg chuyển động ngược lại với vận tốc 120 m/s so với phần còn lại của tên lửa. Hãy xác định vận tốc của mỗi phần sau khi tách.

Lời giải chi tiết:

Chọn hệ khảo sát: Toàn bộ tên lửa. Trong quá trình tách ra, lực nội tại giữa hai phần của tên lửa lớn hơn rất nhiều so với lực tác động từ bên ngoài, do đó hệ được coi là kín theo phương ngang.

Đặt ký hiệu:

• \(m\): Khối lượng tổng cộng của tên lửa trước khi tách.
• \(m_1 = 250\) kg: Khối lượng của phần tách rời.
• \(m_2 = m – m_1 = 350\) kg: Khối lượng của phần còn lại.
• \(v_0 = 120\) m/s: Vận tốc của phần tách rời so với phần còn lại.
• \(v\): Vận tốc của tên lửa trước khi tách.
• \(v_1\): Vận tốc của phần tách rời so với Trái Đất.
• \(v_2\): Vận tốc của phần còn lại sau khi tách.

Mối quan hệ giữa các vận tốc:Vì phần tách rời chuyển động với vận tốc \(v_0 = 120\) m/s ngược lại so với phần còn lại, và theo chiều chuyển động ban đầu của tên lửa, ta có:

\[v_1 = v_2 – v_0\]

– Áp dụng định luật bảo toàn động lượng:

Trước khi tách, động lượng tổng của hệ là:

\[m \cdot v = 600 \cdot 300\]

Sau khi tách, động lượng tổng của hệ được bảo toàn:

\[m \cdot v = m_1 \cdot v_1 + m_2 \cdot v_2\]

Thay \(v_1 = v_2 – v_0\) vào phương trình, ta có:

\[600 \cdot 300 = 250 \cdot (v_2 – 120) + 350 \cdot v_2\]

Giải phương trình này, ta được:

\[180000 = 250v_2 – 30000 + 350v_2\]

\[180000 = 600v_2 – 30000\]

\[600v_2 = 210000\]

\[v_2 = 350 \, \text{m/s}\]

Tính vận tốc \(v_1\) của phần tách rời:

\[v_1 = v_2 – v_0 = 350 – 120 = 230 \, \text{m/s}\]

Kết luận:

• Vận tốc của phần tách rời (khối lượng 250 kg): \(v_1 = 230\) m/s
• Vận tốc của phần còn lại (khối lượng 350 kg): \(v_2 = 350\) m/s

Nhận xét:

• Phần tách rời vẫn tiếp tục di chuyển về phía trước, nhưng với vận tốc nhỏ hơn so với vận tốc ban đầu của tên lửa.
• Phần còn lại của tên lửa có vận tốc lớn hơn so với vận tốc ban đầu, tức là đã được tăng tốc do sự tách rời của phần kia.

Bài tập 4: Một người có khối lượng \(m_1 = 50\) kg đang đứng trên một chiếc thuyền có khối lượng \(m_2 = 200\) kg, nằm yên trên mặt nước phẳng lặng. Người này bắt đầu di chuyển từ mũi thuyền về phía đuôi thuyền với vận tốc \(v_1 = 0,5\) m/s so với thuyền. Biết rằng thuyền dài 3 m và bỏ qua lực cản của nước, hãy trả lời các câu hỏi sau:

a) Tính vận tốc của thuyền đối với mặt nước.

b) Tính quãng đường mà thuyền đã di chuyển trong quá trình người này đi.

c) Khi người này dừng lại, thuyền có tiếp tục chuyển động hay không?

Lời giải chi tiết:

Chọn hệ khảo sát: Người và thuyền. Bỏ qua lực cản của nước, hệ khảo sát được coi là hệ kín vì không có ngoại lực tác dụng lên hệ theo phương ngang.

a) Vận tốc của thuyền đối với mặt nước

• Gọi \(v_1\) là vận tốc của người so với thuyền.
• \(v_2\) là vận tốc của thuyền so với mặt nước.
• \(v_3\) là vận tốc của người so với mặt nước.

Theo công thức cộng vận tốc, ta có:

\[v_3 = v_1 + v_2\]

Chọn chiều dương là chiều người di chuyển, do đó \(v_1 > 0\).

Áp dụng định luật bảo toàn động lượng cho hệ (xét trong hệ quy chiếu gắn với mặt nước):

\[m_1 v_3 + m_2 v_2 = 0\]

Thay \(v_3 = v_1 + v_2\) vào phương trình trên:

\[m_1 (v_1 + v_2) + m_2 v_2 = 0\]

Giải phương trình để tìm \(v_2\):

\[50 (0.5 + v_2) + 200v_2 = 0\]

\[25 + 50v_2 + 200v_2 = 0\]

\[250v_2 = -25\]

\[v_2 = -0.1 \, \text{m/s}\]

Kết quả này cho thấy thuyền chuyển động ngược chiều với người với vận tốc có độ lớn là \(0.1\) m/s.

b) Quãng đường mà thuyền di chuyển

Thời gian người di chuyển từ mũi đến đuôi thuyền là:

\[t = \frac{s_1}{v_1} = \frac{3}{0.5} = 6 \, \text{s}\]

Quãng đường thuyền đi được trong thời gian này là:

\[s_2 = v_2 \cdot t = (-0.1) \times 6 = -0.6 \, \text{m}\]

Giá trị âm của \(s_2\) cho thấy thuyền di chuyển ngược chiều với người, và quãng đường di chuyển của thuyền là \(0.6\) m.

c) Chuyển động của thuyền khi người dừng lại

Khi người ngừng di chuyển (\(v_1 = 0\)), từ công thức bảo toàn động lượng:

\[v_2 = -\frac{m_1 v_1}{m_1 + m_2}\]

Vì \(v_1 = 0\), ta có:

\[v_2 = 0\]

Kết luận: Khi người dừng lại, thuyền cũng ngừng chuyển động.

• Vận tốc của thuyền đối với mặt nước là \(0.1\) m/s theo hướng ngược lại với hướng di chuyển của người.
• Trong khi người di chuyển, thuyền đã đi được quãng đường \(0.6\) m ngược chiều.
• Khi người dừng lại, thuyền cũng dừng lại, không còn chuyển động.

Định luật bảo toàn động lượng không chỉ là một kiến thức lý thuyết khô khan mà còn có những ứng dụng thực tiễn vô cùng rộng rãi. Từ việc giải thích các hiện tượng tự nhiên như va chạm, nổ cho đến việc thiết kế các loại máy móc, phương tiện giao thông, định luật này đều đóng vai trò quan trọng. Hiểu rõ định luật bảo toàn động lượng sẽ giúp bạn có cái nhìn sâu sắc hơn về thế giới xung quanh và trang bị cho mình những kiến thức cần thiết để giải quyết các vấn đề trong cuộc sống.