[Vật lý 12] Hệ số công suất mạch điện xoay chiều: Giải thích chi tiết

Chào mừng các bạn đến với website vatly.edu.vn! Trong bài viết hôm nay, chúng ta sẽ cùng tìm hiểu về một khái niệm quan trọng trong chương trình vật Lý 12: Hệ số công suất của mạch điện xoay chiều.

Hiểu rõ về hệ số công suất không chỉ giúp các bạn nắm vững kiến thức lý thuyết mà còn có thể áp dụng hiệu quả trong thực tiễn. Từ đó, các bạn sẽ biết cách tối ưu hóa hiệu suất sử dụng điện năng, giảm thiểu hao tổn và nâng cao hiệu quả hoạt động của các thiết bị điện. Hãy cùng chúng tôi khám phá chi tiết về hệ số công suất và những ứng dụng thực tiễn của nó nhé!

Hệ số công suất là gì?

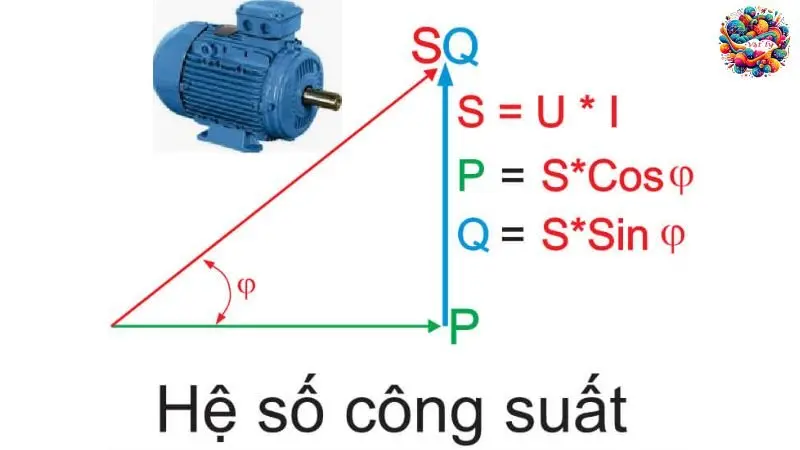
Hệ số công suất (cos phi) là một khái niệm quan trọng trong vật lý và điện học, đặc biệt là trong các hệ thống điện xoay chiều (AC). Nó được định nghĩa là tỷ số giữa công suất thực (P) và công suất biểu kiến (S) trong một mạch điện xoay chiều. Công suất thực là công suất hữu ích thực sự được tiêu thụ hoặc chuyển đổi thành công việc, trong khi công suất biểu kiến là tổng công suất được cung cấp cho mạch.

\[ \cos\varphi = \frac{P}{S} \]

Trong đó:

• \( P \) là công suất hữu ích (đơn vị: watt – W), là phần năng lượng được sử dụng để thực hiện công việc hữu ích.
• \( S \) là công suất toàn phần (đơn vị: volt-ampe – VA), là tổng năng lượng mà mạch điện sử dụng, bao gồm cả phần năng lượng bị tiêu tán trong các thành phần phản kháng.

Trong mạch điện xoay chiều, điện áp và dòng điện có thể lệch pha nhau. Góc lệch pha giữa điện áp và dòng điện được ký hiệu là \( \varphi \). Hệ số công suất \( \cos\varphi \) cho biết mức độ “lệch pha” này, và nó phản ánh hiệu quả sử dụng năng lượng trong mạch:

• Khi \( \varphi = 0^\circ \): Điện áp và dòng điện cùng pha, hệ số công suất \( \cos\varphi = 1 \). Điều này có nghĩa là toàn bộ năng lượng được sử dụng một cách hiệu quả.
• Khi \( \varphi = 90^\circ \): Điện áp và dòng điện lệch pha nhau 90 độ, hệ số công suất \( \cos\varphi = 0 \). Điều này có nghĩa là không có năng lượng nào được sử dụng hữu ích, tất cả đều bị tiêu tán.

Ý nghĩa của hệ số công suất

• Hệ số công suất là một chỉ số quan trọng để đánh giá hiệu quả sử dụng điện năng trong mạch điện.
• Nếu hệ số công suất càng gần 1 (cos φ ≈ 1) thì công suất thực càng lớn so với công suất toàn phần, tức là mạch điện hoạt động hiệu quả hơn.
• Nếu hệ số công suất thấp (cos φ ≈ 0), điều này cho thấy mạch có nhiều công suất phản kháng, dẫn đến hiệu suất sử dụng điện năng thấp.

Các loại công suất trong mạch điện xoay chiều

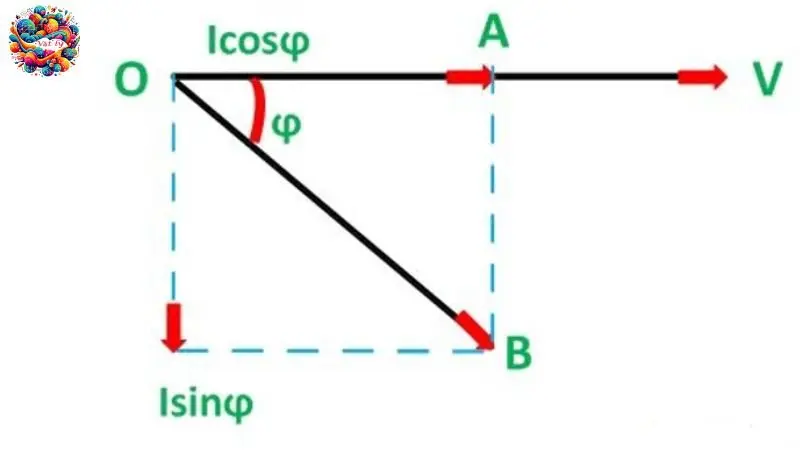
Công suất thực (P)

Công suất thực, còn gọi là công suất hữu ích, là phần công suất được tiêu thụ để thực hiện công việc thực sự như phát sáng, phát nhiệt, hoặc cơ năng. Công suất thực được tính bằng công thức:

\[ P = U \cdot I \cdot \cos(\phi) \]

Trong đó:

• \(P\) là công suất thực (Watt)
• \(U\) là điện áp hiệu dụng (Volt)
• \(I\) là dòng điện hiệu dụng (Ampere)
• \(\cos(\phi)\) là hệ số công suất, với \(\phi\) là góc pha giữa điện áp và dòng điện.

Công suất phản kháng (Q)

Công suất phản kháng là phần công suất không thực hiện công việc hữu ích mà tạo ra từ sự tích lũy năng lượng trong từ trường và điện trường. Công suất phản kháng được tính bằng công thức:

\[ Q = U \cdot I \cdot \sin(\phi) \]

Trong đó:

• \(Q\) là công suất phản kháng (VAR – Volt-Ampere Reactive)
• \(U\) là điện áp hiệu dụng (Volt)
• \(I\) là dòng điện hiệu dụng (Ampere)
• \(\sin(\phi)\) là thành phần phản kháng của góc pha.

Công suất biểu kiến (S)

Công suất biểu kiến là tổng hợp của cả công suất thực và công suất phản kháng, đại diện cho tổng công suất truyền tải trong mạch điện. Công suất biểu kiến được tính bằng công thức:

\[ S = U \cdot I \]

Hoặc theo định lý Pythagore trong tam giác công suất:

\[ S = \sqrt{P^2 + Q^2} \]

Trong đó:

• \(S\) là công suất biểu kiến (VA – Volt-Ampere)
• \(P\) là công suất thực (Watt)
• \(Q\) là công suất phản kháng (VAR)

Công suất trong mạch điện xoay chiều là một yếu tố quan trọng ảnh hưởng đến hiệu suất và hiệu quả sử dụng điện năng. Bằng cách hiểu rõ và quản lý tốt các loại công suất, chúng ta có thể tối ưu hóa hoạt động của hệ thống điện, giảm thiểu hao tổn và tiết kiệm chi phí. Hy vọng bài viết này đã giúp bạn có cái nhìn toàn diện và sâu sắc hơn về công suất trong mạch điện xoay chiều.

Ứng dụng của hệ số công suất trong thực tiễn

Trong hệ thống điện

• Tối ưu hóa truyền tải điện: Hệ số công suất cao giúp giảm hao tổn điện năng trên đường dây, từ đó tăng hiệu suất truyền tải điện.
• Giảm chi phí: Các công ty điện lực thường áp dụng mức phạt cho các doanh nghiệp có hệ số công suất thấp, do đó, cải thiện hệ số công suất giúp giảm chi phí điện năng.

Trong các thiết bị điện

• Hiệu suất thiết bị: Thiết bị điện có hệ số công suất cao sẽ hoạt động hiệu quả hơn, giảm thiểu lượng điện năng lãng phí dưới dạng nhiệt.
• Tuổi thọ thiết bị: Cải thiện hệ số công suất giúp kéo dài tuổi thọ của các thiết bị điện nhờ giảm thiểu hao mòn và quá nhiệt.

Trong công nghiệp

• Tăng năng suất: Các máy móc và thiết bị trong các nhà máy hoạt động hiệu quả hơn khi hệ số công suất được cải thiện.
• Giảm thiểu sự cố: Hệ số công suất cao giúp giảm nguy cơ sự cố liên quan đến quá tải hoặc ngắn mạch, đảm bảo quá trình sản xuất không bị gián đoạn.

Bài tập về hệ số công suất của mạch điện xoay chiều – Vật lý 12

Bài tập 1: Cho mạch điện RLC nối tiếp gồm điện trở \( R = 50 \Omega \), cuộn cảm \( L = 0,2 H \) và tụ điện \( C = 10 \mu F \). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \( u = 220\sqrt{2} \sin(100\pi t) \) (V). Tính hệ số công suất của mạch.

Hướng dẫn lời giải chi tiết:

• Tần số góc: \( \omega = 100\pi \) (rad/s)
• Dung kháng: \( X_C = \frac{1}{\omega C} = \frac{1}{100\pi \cdot 10^{-5}} = 318 \Omega \)
• Cảm kháng: \( X_L = \omega L = 100\pi \cdot 0,2 = 62,8 \Omega \)
• Tổng trở: \( Z = \sqrt{R^2 + (X_L – X_C)^2} = \sqrt{50^2 + (62,8 – 318)^2} = \sqrt{50^2 + (-255,2)^2} = 260,2 \Omega \)
• Hệ số công suất: \( \cos\varphi = \frac{R}{Z} = \frac{50}{260,2} \approx 0,192 \)

Bài tập 2: Cho mạch điện chỉ chứa điện trở \( R = 100 \Omega \). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \( u = 220\sqrt{2} \sin(120\pi t) \) (V). Tính hệ số công suất của mạch.

Hướng dẫn lời giải chi tiết:

• Trong mạch chỉ chứa điện trở, hệ số công suất luôn là 1.
• Hệ số công suất: \( \cos\varphi = 1 \)

Bài tập 3: Cho mạch điện chỉ chứa cuộn cảm \( L = 0,1 H \). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \( u = 110\sqrt{2} \sin(50\pi t) \) (V). Tính hệ số công suất của mạch.

Hướng dẫn lời giải chi tiết:

• Tần số góc: \( \omega = 50\pi \) (rad/s)
• Cảm kháng: \( X_L = \omega L = 50\pi \cdot 0,1 = 5\pi \approx 15,7 \Omega \)
• Trong mạch chỉ chứa cuộn cảm, điện áp và dòng điện lệch pha nhau 90 độ.
• Hệ số công suất: \( \cos\varphi = \cos 90^\circ = 0 \)

Bài tập 4: Cho mạch điện chỉ chứa tụ điện \( C = 20 \mu F \). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \( u = 220\sqrt{2} \sin(100\pi t) \) (V). Tính hệ số công suất của mạch.

Hướng dẫn lời giải chi tiết:

• Tần số góc: \( \omega = 100\pi \) (rad/s)
• Dung kháng: \( X_C = \frac{1}{\omega C} = \frac{1}{100\pi \cdot 20 \cdot 10^{-6}} = 159 \Omega \)
• Trong mạch chỉ chứa tụ điện, điện áp và dòng điện lệch pha nhau 90 độ.
• Hệ số công suất: \( \cos\varphi = \cos 90^\circ = 0 \)

Bài tập 5: Cho mạch điện nối tiếp gồm điện trở \( R = 100 \Omega \) và cuộn cảm \( L = 0,5 H \). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \( u = 220\sqrt{2} \sin(50\pi t) \) (V). Tính hệ số công suất của mạch.

Hướng dẫn lời giải chi tiết:

• Tần số góc: \( \omega = 50\pi \) (rad/s)
• Cảm kháng: \( X_L = \omega L = 50\pi \cdot 0,5 = 25\pi \approx 78,5 \Omega \)
• Tổng trở: \( Z = \sqrt{R^2 + X_L^2} = \sqrt{100^2 + 78,5^2} = 126,7 \Omega \)
• Hệ số công suất: \( \cos\varphi = \frac{R}{Z} = \frac{100}{126,7} \approx 0,79 \)

Bài tập 6: Cho mạch điện RLC song song gồm điện trở \( R = 40 \Omega \), cuộn cảm \( L = 0,1 H \), và tụ điện \( C = 20 \mu F \). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \( u = 200\sqrt{2} \sin(100\pi t) \) (V). Tính hệ số công suất của mạch.

Hướng dẫn lời giải chi tiết:

• Tần số góc: \( \omega = 100\pi \) (rad/s)
• Dung kháng: \( X_C = \frac{1}{\omega C} = \frac{1}{100\pi \cdot 20 \cdot 10^{-6}} = 159 \Omega \)
• Cảm kháng: \( X_L = \omega L = 100\pi \cdot 0,1 = 31,4 \Omega \)
• Tổng dẫn kháng: \( Y = \sqrt{\left(\frac{1}{R}\right)^2 + \left(\frac{1}{X_L} – \frac{1}{X_C}\right)^2} = \sqrt{\left(\frac{1}{40}\right)^2 + \left(\frac{1}{31,4} – \frac{1}{159}\right)^2} \approx 0,025 S \)
• Tổng trở: \( Z = \frac{1}{Y} = 40 \Omega \)
• Hệ số công suất: \( \cos\varphi = \frac{R}{Z} = 1 \)

Bài tập 7: Cho mạch điện RLC nối tiếp gồm điện trở \( R = 50 \Omega \), cuộn cảm \( L = 0,2 H \) và tụ điện \( C = 10 \mu F \). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \( u = 220\sqrt{2} \sin(100\pi t) \) (V). Tính hệ số công suất khi tần số góc thay đổi từ 100π rad/s lên 200π rad/s.

Hướng dẫn lời giải chi tiết:

Tần số góc ban đầu: \( \omega = 100\pi \) (rad/s)

• Dung kháng: \( X_C = \frac{1}{\omega C} = \frac{1}{100\pi \cdot 10^{-5}} = 318 \Omega \)
• Cảm kháng: \( X_L = \omega L = 100\pi \cdot 0,2 = 62,8 \Omega \)
• Tổng trở: \( Z = \sqrt{R^2 + (X_L – X_C)^2} = \sqrt{50^2 + (62,8 – 318)^2} = \sqrt{50^2 + (-255,2)^2} = 260,2 \Omega \)
• Hệ số công suất: \( \cos\varphi = \frac{R}{Z} = \frac{50}{260,2} \approx 0,192 \)

Tần số góc mới: \( \omega = 200\pi \) (rad/s)

• Dung kháng: \( X_C = \frac{1}{\omega C} = \frac{1}{200\pi \cdot 10^{-5}} = 159 \Omega \)
• Cảm kháng: \( X_L = \omega L = 200\pi \cdot 0,2 = 125,6 \Omega \)
• Tổng trở: \( Z = \sqrt{R^2 + (X_L – X_C)^2} = \sqrt{50^2 + (125,6 – 159)^2} = \sqrt{50^2 + (-33,4)^2} = 60,1 \Omega \)
• Hệ số công suất: \( \cos\varphi = \frac{R}{Z} = \frac{50}{60,1} \approx 0,832 \)

Bài tập 8: Cho mạch điện nối tiếp gồm hai điện trở \( R_1 = 30 \Omega \), \( R_2 = 40 \Omega \) và một tụ điện \( C = 50 \mu F \). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \( u = 100\sqrt{2} \sin(120\pi t) \) (V). Tính hệ số công suất của mạch.

Hướng dẫn lời giải chi tiết:

• Tần số góc: \( \omega = 120\pi \) (rad/s)
• Dung kháng: \( X_C = \frac{1}{\omega C} = \frac{1}{120\pi \cdot 50 \cdot 10^{-6}} \approx 53,1 \Omega \)
• Tổng điện trở: \( R_t = R_1 + R_2 = 30 + 40 = 70 \Omega \)
• Tổng trở: \( Z = \sqrt{R_t^2 + X_C^2} = \sqrt{70^2 + 53,1^2} \approx 88,2 \Omega \)
• Hệ số công suất: \( \cos\varphi = \frac{R_t}{Z} = \frac{70}{88,2} \approx 0,794 \)

Bài 9: Cho mạch điện gồm cuộn cảm \( L = 0,5 H \) và tụ điện \( C = 20 \mu F \) nối tiếp. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \( u = 200\sqrt{2} \sin(100\pi t) \) (V). Tính hệ số công suất của mạch.

Hướng dẫn lời giải chi tiết:

• Tần số góc: \( \omega = 100\pi \) (rad/s)
• Dung kháng: \( X_C = \frac{1}{\omega C} = \frac{1}{100\pi \cdot 20 \cdot 10^{-6}} = 159 \Omega \)
• Cảm kháng: \( X_L = \omega L = 100\pi \cdot 0,5 = 157 \Omega \)
• Tổng trở: \( Z = \sqrt{(X_L – X_C)^2} = \sqrt{(157 – 159)^2} = 2 \Omega \)
• Hệ số công suất: \( \cos\varphi = 0 \) (do \( R = 0 \) trong mạch LC nối tiếp)

Bài tập 10: Cho mạch điện gồm điện trở \( R = 60 \Omega \), cuộn cảm \( L = 0,3 H \) và tụ điện \( C = 30 \mu F \) nối tiếp, trong đó cuộn cảm \( L \) và điện trở \( R \) mắc song song với nhau. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \( u = 220\sqrt{2} \sin(50\pi t) \) (V). Tính hệ số công suất của mạch.

Hướng dẫn lời giải chi tiết:

• Tần số góc: \( \omega = 50\pi \) (rad/s)
• Dung kháng: \( X_C = \frac{1}{\omega C} = \frac{1}{50\pi \cdot 30 \cdot 10^{-6}} \approx 212,2 \Omega \)
• Cảm kháng: \( X_L = \omega L = 50\pi \cdot 0,3 = 47,1 \Omega \)
• Tổng kháng của R và L song song: \( Z_{RL} = \frac{R \cdot X_L}{\sqrt{R^2 + X_L^2}} = \frac{60 \cdot 47,1}{\sqrt{60^2 + 47,1^2}} \approx 37,8 \Omega \)
• Tổng trở: \( Z = \sqrt{Z_{RL}^2 + X_C^2} = \sqrt{37,8^2 + 212,2^2} \approx 215,6 \Omega \)
• Hệ số công suất: \( \cos\varphi = \frac{Z_{RL}}{Z} = \frac{37,8}{215,6} \approx 0,175 \)

Qua bài viết này, hy vọng các bạn đã có cái nhìn rõ ràng hơn về hệ số công suất của mạch điện xoay chiều, một phần kiến thức quan trọng trong chương trình Vật Lý 12. Nắm vững hệ số công suất không chỉ giúp các bạn đạt kết quả tốt trong học tập mà còn mang lại nhiều lợi ích khi áp dụng vào thực tế. Hãy tiếp tục theo dõi vatly.edu.vn để cập nhật thêm nhiều kiến thức bổ ích và những bài học thú vị khác về vật lý. Cảm ơn các bạn đã dành thời gian đọc bài viết, chúc các bạn học tập thật tốt và thành công!