Lý thuyết Vật lý 10 –  Sai số của phép đo các đại lượng vật lí 

Chào mừng bạn đến với vatly.edu.vn, địa chỉ tin cậy cung cấp kiến thức và tài liệu vật lý cho học sinh và giáo viên. Hôm nay, chúng tôi sẽ cùng bạn tìm hiểu về một chủ đề quan trọng trong việc thực hiện các thí nghiệm vật lý: Sai số của phép đo các đại lượng vật lí. Sai số là yếu tố không thể tránh khỏi trong quá trình đo lường và ảnh hưởng lớn đến độ chính xác của kết quả thí nghiệm. Bài viết này sẽ giúp bạn hiểu rõ các loại sai số, nguyên nhân và cách giảm thiểu chúng để đạt được kết quả đo lường chính xác nhất.

Phép đo các đại lượng vật lí và hệ đơn vị SI

Phép đo các đại lượng vật lí

• Phép đo các đại lượng vật lí là quá trình so sánh chúng với một đơn vị đã được quy ước sẵn.
• Sử dụng các dụng cụ đo trực tiếp để so sánh và xác định giá trị của đại lượng vật lí gọi là phép đo trực tiếp.
• Khi xác định giá trị của một đại lượng vật lí thông qua công thức liên hệ với các đại lượng đo trực tiếp, đó là phép đo gián tiếp.

Đơn vị đo

– Hệ đơn vị đo lường thường được sử dụng là hệ đơn vị SI.

– Hệ đơn vị SI là hệ thống đo lường quốc tế được thống nhất và áp dụng rộng rãi trên toàn thế giới.

Hệ SI bao gồm 7 đơn vị cơ bản:

• Độ dài: mét (m)
• Nhiệt độ: kelvin (K)
• Thời gian: giây (s)
• Cường độ dòng điện: ampe (A)
• Khối lượng: kilogram (kg)
• Cường độ sáng: candela (cd)
• Lượng chất: mol (mol)

Sai số phép đo

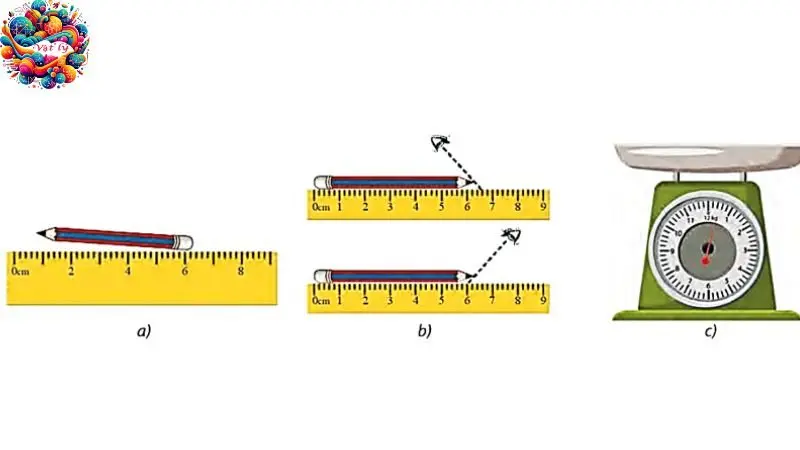
Phân loại sai số

Sai số hệ thống: Sai số hệ thống là sự sai lệch do các yếu tố như độ chia không chính xác của dụng cụ đo (\( \Delta A’ \)) hoặc do điểm 0 ban đầu bị lệch. Sai số dụng cụ \( \Delta A’ \) thường được tính bằng nửa hoặc một độ chia trên dụng cụ đo.

Sai số ngẫu nhiên: Sai số ngẫu nhiên là sự sai lệch do giới hạn của khả năng giác quan con người và tác động của các yếu tố ngẫu nhiên bên ngoài.

Giá trị trung bình

Giá trị trung bình khi đo nhiều lần một đại lượng \( A \) được tính bằng công thức:

\[ \bar{A} = \frac{A_1 + A_2 + … + A_n}{n} \]

Giá trị này được coi là gần đúng nhất với giá trị thực của đại lượng \( A \).

Cách xác định sai số của phép đo

Sai số tuyệt đối của mỗi lần đo là trị tuyệt đối của hiệu giữa giá trị trung bình và giá trị của mỗi lần đo:

\[ \Delta A_1 = |\bar{A} – A_1| \]

\[ \Delta A_2 = |\bar{A} – A_2| \]

\[ \Delta A_3 = |\bar{A} – A_3| \]

Sai số tuyệt đối trung bình của \( n \) lần đo, còn gọi là sai số ngẫu nhiên, được tính bằng:

\[ \bar{\Delta A} = \frac{\Delta A_1 + \Delta A_2 + … + \Delta A_n}{n} \]

Sai số tuyệt đối của phép đo là tổng của sai số ngẫu nhiên và sai số dụng cụ:

\[ \Delta A = \bar{\Delta A} + \Delta A’ \]

Trong đó, sai số dụng cụ \( \Delta A’ \) thường được lấy bằng nửa hoặc một độ chia nhỏ nhất trên dụng cụ đo.

Cách viết kết quả đo

Kết quả đo đại lượng \( A \) được viết dưới dạng:

\[ A = \bar{A} \pm \Delta A \]

Trong đó:

• \( \Delta A \) được làm tròn đến hai chữ số có nghĩa.
• \( \bar{A} \) được viết với độ chính xác tương ứng theo bậc thập phân của \( \Delta A\).

Sai số tỉ đối

Sai số tỉ đối \( \delta A \) của phép đo là tỷ lệ giữa sai số tuyệt đối và giá trị trung bình của đại lượng đo, tính theo phần trăm:

\[ \delta A = \left( \frac{\Delta A}{\bar{A}} \right) \times 100\% \]

Cách xác định sai số của phép đo gián tiếp

• Sai số tuyệt đối của một tổng hay hiệu bằng tổng các sai số tuyệt đối của các số hạng.
• Sai số tỉ đối của một tích hay thương bằng tổng các sai số tỉ đối của các thừa số.
• Nếu công thức xác định đại lượng đo gián tiếp chứa các hằng số, thì hằng số phải được lấy đến phần thập phân lẻ nhỏ hơn 1/10 tổng các sai số trong cùng công thức tính.
• Nếu công thức xác định đại lượng đo gián tiếp phức tạp và các dụng cụ đo trực tiếp có độ chính xác cao, có thể bỏ qua sai số dụng cụ.

Bài tập ứng dụng về sai số của phép đo các đại lượng vật lý 

Bài tập 1: Một học sinh đo chiều dài của một cái bàn 5 lần và thu được các giá trị: 1.20 m, 1.18 m, 1.19 m, 1.21 m, 1.20 m. Hãy tính giá trị trung bình, sai số tuyệt đối và sai số tỉ đối của phép đo.

Lời giải:

• Giá trị trung bình:

\[ \bar{A} = \frac{1.20 + 1.18 + 1.19 + 1.21 + 1.20}{5} = 1.196 \, \text{m} \]

• Sai số tuyệt đối:

\[ \Delta A_1 = |\bar{A} – 1.20| = |1.196 – 1.20| = 0.004 \, \text{m} \]

\[ \Delta A_2 = |\bar{A} – 1.18| = |1.196 – 1.18| = 0.016 \, \text{m} \]

\[ \Delta A_3 = |\bar{A} – 1.19| = |1.196 – 1.19| = 0.006 \, \text{m} \]

\[ \Delta A_4 = |\bar{A} – 1.21| = |1.196 – 1.21| = 0.014 \, \text{m} \]

\[ \Delta A_5 = |\bar{A} – 1.20| = |1.196 – 1.20| = 0.004 \, \text{m} \]

\[ \bar{\Delta A} = \frac{0.004 + 0.016 + 0.006 + 0.014 + 0.004}{5} = 0.0088 \, \text{m} \]

• Sai số tỉ đối:

\[ \delta A = \left( \frac{\bar{\Delta A}}{\bar{A}} \right) \times 100\% = \left( \frac{0.0088}{1.196} \right) \times 100\% \approx 0.736\% \]

Kết quả đo: 

\[ A = 1.196 \pm 0.0088 \, \text{m} \]

Sai số tỉ đối: 

\[ \delta A \approx 0.736\% \]

Bài tập 2: Cho biết khối lượng \( m = 2.00 \pm 0.01 \, \text{kg} \) và thể tích \( V = 0.50 \pm 0.02 \, \text{m}^3 \). Tính khối lượng riêng \( \rho \) và sai số của nó.

Lời giải:

• Công thức khối lượng riêng:

\[ \rho = \frac{m}{V} \]

• Giá trị trung bình:

\[ \bar{\rho} = \frac{\bar{m}}{\bar{V}} = \frac{2.00}{0.50} = 4.00 \, \text{kg/m}^3 \]

• Sai số tỉ đối của \( m \) và \( V \):

\[ \delta m = \left( \frac{\Delta m}{\bar{m}} \right) \times 100\% = \left( \frac{0.01}{2.00} \right) \times 100\% = 0.5\% \]

\[ \delta V = \left( \frac{\Delta V}{\bar{V}} \right) \times 100\% = \left( \frac{0.02}{0.50} \right) \times 100\% = 4\% \]

• Sai số tỉ đối của \( \rho \):

\[ \delta \rho = \delta m + \delta V = 0.5\% + 4\% = 4.5\% \]

• Sai số tuyệt đối của \( \rho \):

\[ \Delta \rho = \left( \frac{\delta \rho}{100} \right) \times \bar{\rho} = \left( \frac{4.5}{100} \right) \times 4.00 = 0.18 \, \text{kg/m}^3 \]

Kết quả đo: 

\[ \rho = 4.00 \pm 0.18 \, \text{kg/m}^3 \]

Bài tập 3: Một thanh gỗ có chiều dài \( l_1 = 3.50 \pm 0.05 \, \text{m} \) được ghép nối với một thanh gỗ khác có chiều dài \( l_2 = 2.00 \pm 0.03 \, \text{m} \). Tính chiều dài tổng cộng \( l \) và sai số của nó.

Lời giải:

• Chiều dài tổng cộng:

\[ l = l_1 + l_2 = 3.50 + 2.00 = 5.50 \, \text{m} \]

• Sai số tuyệt đối tổng cộng:

\[ \Delta l = \Delta l_1 + \Delta l_2 = 0.05 + 0.03 = 0.08 \, \text{m} \]

Kết quả đo: 

\[ l = 5.50 \pm 0.08 \, \text{m} \]

Hy vọng rằng qua bài viết này, bạn đã nắm vững kiến thức về sai số của phép đo các đại lượng vật lí và biết cách xử lý chúng để nâng cao độ chính xác trong các thí nghiệm. Đừng quên truy cập vatly.edu.vn thường xuyên để cập nhật thêm nhiều bài viết hữu ích và tài liệu chất lượng về vật lý. Chúng tôi luôn sẵn sàng hỗ trợ bạn trên con đường chinh phục tri thức và khám phá thế giới khoa học đầy thú vị!