Chinh phục Vật lý 6: Khám phá mặt phẳng nghiêng từ A đến Z
Mặt phẳng nghiêng là một trong những khái niệm cơ bản và quan trọng trong chương trình Vật lý lớp 6. Đây là một dạng máy cơ đơn giản nhưng có ứng dụng rộng rãi trong đời sống hàng ngày và các lĩnh vực kỹ thuật.
Mặt phẳng nghiêng là một trong những khái niệm cơ bản và quan trọng trong chương trình Vật lý lớp 6. Đây là một dạng máy cơ đơn giản nhưng có ứng dụng rộng rãi trong đời sống hàng ngày và các lĩnh vực kỹ thuật. Hiểu rõ về mặt phẳng nghiêng không chỉ giúp học sinh nắm vững kiến thức cơ bản của vật lý mà còn phát triển khả năng tư duy và ứng dụng vào thực tiễn. Bài viết này trên vatly.edu.vn sẽ cung cấp một cái nhìn toàn diện về mặt phẳng nghiêng, từ định nghĩa, công thức tính toán đến các bài tập thực hành cụ thể.
Tìm hiểu mặt phẳng nghiêng là gì?
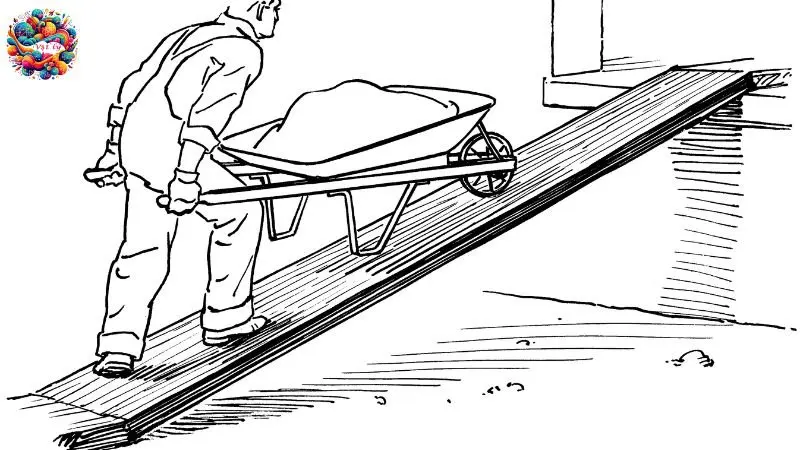
Mặt phẳng nghiêng là một trong những máy cơ đơn giản được sử dụng để nâng hoặc di chuyển vật thể lên một độ cao nhất định một cách dễ dàng hơn. Nó là một bề mặt phẳng được đặt nghiêng so với mặt đất, tạo ra một góc với mặt phẳng ngang.
Đặc điểm của mặt phẳng nghiêng
- Hình dạng: Một bề mặt phẳng và dài.
- Góc nghiêng: Tạo một góc với mặt phẳng ngang, giúp giảm lực cần thiết để nâng vật lên.
- Độ dài: Độ dài của mặt phẳng càng lớn thì góc nghiêng càng nhỏ, và ngược lại.
Ví dụ về mặt phẳng nghiêng
- Cầu thang: Giúp con người di chuyển lên xuống giữa các tầng một cách dễ dàng.
- Đường dốc: Sử dụng trong vận tải để xe cộ dễ dàng lên xuống giữa các độ cao khác nhau.
- Máy dốc dùng trong công nghiệp: Để di chuyển hàng hóa hoặc nguyên liệu giữa các bề mặt có độ cao khác nhau.
Lực cần thiết để đẩy hoặc kéo một vật lên mặt phẳng nghiêng có thể được tính bằng công thức sau:
\[ F = \frac{W \times h}{l} \]
Trong đó:
- \( F \) là lực cần thiết.
- \( W \) là trọng lượng của vật.
- \( h \) là chiều cao cần nâng vật lên.
- \( l \) là chiều dài của mặt phẳng nghiêng.
Lợi ích của mặt phẳng nghiêng
Mặt phẳng nghiêng là một công cụ đơn giản nhưng rất hiệu quả trong việc giảm bớt sức lao động và tối ưu hóa công việc. Dưới đây là những lợi ích chính của mặt phẳng nghiêng:
Giảm lực cần thiết để nâng vật nặng: Khi sử dụng mặt phẳng nghiêng, lực cần thiết để nâng vật nặng lên độ cao mong muốn được giảm đáng kể so với việc nâng trực tiếp. Điều này giúp tiết kiệm sức lực và làm việc hiệu quả hơn.
Tăng hiệu quả công việc: Bằng cách sử dụng mặt phẳng nghiêng, con người và máy móc có thể di chuyển vật liệu và hàng hóa một cách dễ dàng và nhanh chóng hơn. Điều này tăng cường hiệu quả làm việc và giảm thời gian hoàn thành công việc.
Ứng dụng đa dạng trong đời sống và công nghiệp: Mặt phẳng nghiêng được sử dụng rộng rãi trong nhiều lĩnh vực như xây dựng, vận tải, và sản xuất công nghiệp. Ví dụ, cầu thang, dốc lên xuống cho xe cộ, và băng tải trong các nhà máy đều là ứng dụng của mặt phẳng nghiêng.
An toàn hơn cho người sử dụng: Việc di chuyển vật nặng bằng mặt phẳng nghiêng giảm nguy cơ chấn thương so với việc nâng vật trực tiếp. Điều này đặc biệt quan trọng trong môi trường làm việc yêu cầu vận chuyển nhiều hàng hóa nặng.
Mặt phẳng nghiêng là một công cụ đơn giản nhưng mang lại rất nhiều lợi ích thiết thực trong đời sống hàng ngày cũng như trong các ứng dụng công nghiệp. Việc sử dụng mặt phẳng nghiêng không chỉ giúp tiết kiệm sức lao động mà còn tăng cường hiệu quả công việc và đảm bảo an toàn cho người sử dụng.
Phương pháp giải bài tập về mặt phẳng nghiêng
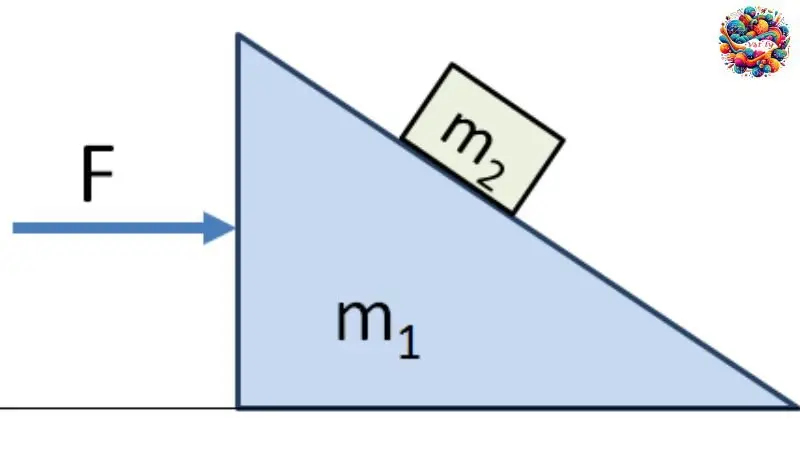
Dưới đây là các bước phương pháp giải và ví dụ cụ thể:
1. Xác định các đại lượng cơ bản
- Chiều dài mặt phẳng nghiêng (l): Chiều dài của bề mặt nghiêng từ chân đến đỉnh.
- Chiều cao của mặt phẳng nghiêng (h): Độ cao từ chân đến đỉnh của mặt phẳng nghiêng.
- Lực kéo (F): Lực cần thiết để kéo vật lên mặt phẳng nghiêng.
- Trọng lượng của vật (P): Lực trọng trường tác động lên vật, thường được tính bằng \( P = m \cdot g \), trong đó \( m \) là khối lượng và \( g \) là gia tốc trọng trường (thường lấy là 9.8 m/s² hoặc 10 m/s² tùy theo bài toán).
2. Sử dụng các công thức liên quan
– Công thức tính lực kéo trên mặt phẳng nghiêng không có ma sát:
\[ F = \frac{P \cdot h}{l} \]
Trong đó \( F \) là lực kéo, \( P \) là trọng lượng của vật, \( h \) là chiều cao của mặt phẳng nghiêng và \( l \) là chiều dài của mặt phẳng nghiêng.
– Công thức tính công của lực kéo (A):
\[ A = F \cdot l \]
Trong đó \( A \) là công, \( F \) là lực kéo và \( l \) là chiều dài của mặt phẳng nghiêng.
Ví dụ minh hoạ
Bài 1: Một vật có trọng lượng 50 N được kéo lên trên một mặt phẳng nghiêng có chiều dài 4 m và chiều cao 1 m. Tính lực kéo cần thiết để kéo vật lên mặt phẳng nghiêng.
Bước 1: Đọc kỹ đề bài
- Trọng lượng vật \( P = 50 \, N \)
- Chiều dài mặt phẳng nghiêng \( l = 4 \, m \)
- Chiều cao mặt phẳng nghiêng \( h = 1 \, m \)
Bước 2: Áp dụng công thức
\[ F = \frac{P \cdot h}{l} = \frac{50 \cdot 1}{4} = 12.5 \, N \]
=> Lực kéo cần thiết để kéo vật lên mặt phẳng nghiêng là 12.5 N.
Bài 2: Tính công thực hiện để kéo vật nặng 50 N lên trên mặt phẳng nghiêng dài 4 m với lực kéo 12.5 N.
Bước 1: Đọc kỹ đề bài
- Lực kéo \( F = 12.5 \, N \)
- Chiều dài mặt phẳng nghiêng \( l = 4 \, m \)
Bước 2: Áp dụng công thức tính công
\[ A = F \cdot l = 12.5 \cdot 4 = 50 \, J \]
=> Công thực hiện để kéo vật lên mặt phẳng nghiêng là 50 J.
Lưu ý khi giải bài tập
– Luôn kiểm tra đơn vị của các đại lượng trước khi thực hiện phép tính.
– Trong một số bài toán có thể có thêm yếu tố ma sát, cần xem xét lực ma sát khi áp dụng công thức.
– Luôn vẽ hình minh họa để dễ dàng hình dung và xác định các đại lượng liên quan.
Ứng dụng của mặt phẳng nghiêng trong thực tiễn

Mặt phẳng nghiêng là một trong sáu loại máy đơn giản cổ điển, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau để giảm bớt lực cần thiết cho việc nâng hoặc di chuyển các vật nặng. Dưới đây là một số ứng dụng phổ biến của mặt phẳng nghiêng trong thực tiễn:
- Xây dựng: Mặt phẳng nghiêng được sử dụng để nâng các vật liệu xây dựng nặng như gạch, đá hay bê tông lên cao. Thay vì nâng trực tiếp, công nhân có thể sử dụng mặt phẳng nghiêng để kéo vật liệu lên một cách dễ dàng hơn, tiết kiệm sức lực và an toàn hơn.
- Vận chuyển: Trong ngành vận tải, ramp (một dạng mặt phẳng nghiêng) được sử dụng để tải và dỡ hàng hóa từ xe tải hoặc container. Điều này làm giảm lực cần thiết để di chuyển hàng hóa và giảm nguy cơ chấn thương cho người lao động.
- Thiết kế nội thất và kiến trúc: Mặt phẳng nghiêng không chỉ hữu ích trong việc di chuyển vật nặng mà còn được tích hợp vào thiết kế các tòa nhà để tạo điều kiện dễ dàng tiếp cận cho mọi người, đặc biệt là những người sử dụng xe lăn.
- Sản xuất công nghiệp: Trong các nhà máy và dây chuyền sản xuất, mặt phẳng nghiêng giúp di chuyển các thành phần nặng từ một bước của quy trình sản xuất sang bước tiếp theo, giảm thiểu nhu cầu sử dụng thiết bị nâng đỡ cồng kềnh.
- Thể thao và giải trí: Các ramp cũng được sử dụng trong các môn thể thao như skateboarding, bmx hoặc trong các công viên giải trí để tạo ra các đường trượt và bán nguyệt cho người chơi.
Mặt phẳng nghiêng là một công cụ đơn giản nhưng cực kỳ hiệu quả, giúp giảm lực lao động và tăng hiệu quả công việc, từ đó là một phần không thể thiếu trong cuộc sống hàng ngày và công nghiệp.
Bài tập ứng dụng về mặt phẳng nghiêng (Có đáp án)

Câu 1: Phát biểu nào sau đây là sai về mặt phẳng nghiêng?
A. Mặt phẳng nghiêng giúp ta lợi về lực, thiệt về đường đi và lợi về công.
B. Hiệu suất của mặt phẳng nghiêng phụ thuộc vào độ dốc của nó.
C. Mặt phẳng nghiêng không cho ta lợi về lực.
D. Mặt phẳng nghiêng càng dài thì lực kéo vật lên càng nhỏ.
Đáp án: C
Câu 2. Một người dùng mặt phẳng nghiêng để kéo một thùng hàng nặng 100kg lên cao 2m. Biết chiều dài mặt phẳng nghiêng là 10m và lực ma sát bằng 20% trọng lực của vật. Lực kéo cần thiết để thực hiện việc này là:
A. 120N.
B. 140N.
C. 160N.
D. 180N.
Đáp án: B
Câu 3. Một xe máy có khối lượng 150kg đang lên dốc bằng một mặt phẳng nghiêng dài 16m cao 3m. Lực kéo cần thiết để xe máy lên dốc là (bỏ qua lực ma sát):
A. 1125N.
B. 1250N.
C. 1375N.
D. 1500N.
Đáp án: C
Câu 4. Một kiện hàng có khối lượng 50kg được kéo lên cao 1m bằng mặt phẳng nghiêng dài 10m. Lực cần thiết để kéo vật lên bằng mặt phẳng nghiêng này là (bỏ qua lực ma sát):
A. 50N.
B. 100N.
C. 250N.
D. 500N.
Đáp án: B
Câu 5. Trong các trường hợp sau, trường hợp nào không sử dụng mặt phẳng nghiêng?
A. Dùng tấm ván để đưa xe máy lên bậc thềm.
B. Kéo xe bò lên dốc.
C. Dùng ròng rọc để đưa vật lên cao.
D. Dùng thang để lên gác mái.
Đáp án: C
Câu 6. Một người dùng mặt phẳng nghiêng dài 10m để kéo một vật có khối lượng 50kg lên cao 2m. Lực ma sát giữa vật và mặt phẳng nghiêng là 10N. Hiệu suất của mặt phẳng nghiêng trong trường hợp này là:
A. 40%.
B. 50%.
C. 60%.
D. 70%.
Đáp án: D
Câu 7. Một kiện hàng có khối lượng 70kg được kéo lên cao 3m bằng mặt phẳng nghiêng dài 14m. Bỏ qua lực ma sát, lực cần thiết để kéo vật lên bằng mặt phẳng nghiêng này là:
A. 150N.
B. 210N.
C. 245N.
D. 280N.
Đáp án: C
Câu 8. Một xe máy có khối lượng 100kg đang lên dốc bằng một mặt phẳng nghiêng dài 18m cao 4m. Lực kéo cần thiết để xe máy lên dốc (bỏ qua lực ma sát) là:
A. 800N.
B. 900N.
C. 1000N.
D. 1100N.
Đáp án: C
Câu 9. Một người muốn dùng mặt phẳng nghiêng để đưa một thùng hàng nặng 120kg lên cao 1,5m. Người đó có thể sử dụng mặt phẳng nghiêng nào sau đây với lực kéo nhỏ nhất (bỏ qua lực ma sát)?
A. Mặt phẳng nghiêng dài 6m.
B. Mặt phẳng nghiêng dài 8m.
C. Mặt phẳng nghiêng dài 10m.
D. Mặt phẳng nghiêng dài 12m.
Đáp án: A
Câu 10. Một kiện hàng có khối lượng 60kg được kéo lên cao 2m bằng mặt phẳng nghiêng dài 12m. Lực cần thiết để kéo vật lên bằng mặt phẳng nghiêng này bằng cách nào sau đây là có lợi nhất về mặt lực (bỏ qua lực ma sát)?
A. Kéo vật trực tiếp theo phương dốc.
B. Sử dụng một palăng gồm 1 ròng rọc động và 1 ròng rọc cố định.
C. Sử dụng mặt phẳng nghiêng dài 6m để kéo vật lên cao 1m, sau đó kéo tiếp vật lên cao 1m bằng mặt phẳng phẳng.
D. Sử dụng mặt phẳng nghiêng dài 8m để kéo vật lên cao 1m, sau đó kéo tiếp vật lên cao 1m bằng mặt phẳng phẳng.
Đáp án: C
Mặt phẳng nghiêng là một công cụ hữu ích giúp giảm bớt sức lao động và tối ưu hóa hiệu quả công việc. Việc nắm vững khái niệm và ứng dụng của mặt phẳng nghiêng không chỉ giúp các em học sinh lớp 6 hiểu sâu hơn về vật lý mà còn có thể áp dụng vào nhiều tình huống thực tế trong cuộc sống. Hãy tiếp tục theo dõi vatly.edu.vn để cập nhật thêm nhiều kiến thức bổ ích và các bài tập thú vị khác trong môn Vật lý. Chúc các em học tập tốt và thành công!
Bài Viết Liên Quan
Tôi là Kiều Anh, đam mê khám phá và chia sẻ những kiến thức vật lý thú vị từ cuộc sống hằng ngày đến bài học trên lớp. Với cách viết sinh động và dễ hiểu, tôi mong muốn giúp độc giả thấy được vẻ đẹp của vật lý trong mọi khía cạnh của cuộc sống. Hy vọng những bài viết của tôi trên vatly.edu.vn sẽ truyền cảm hứng và làm giàu thêm kiến thức cho mọi người.







