Giải mã phương trình trạng thái khí lý tưởng chi tiết nhất
Khám phá phương trình trạng thái khí lý tưởng tại vatly.edu.vn – một cánh cổng dẫn đến hiểu biết sâu sắc về nguyên lý cơ bản trong vật lý. Bài viết này sẽ mang đến cho bạn cái nhìn chính xác về cách thức hoạt động của vũ trụ qua lăng kính vật lý.
Phương trình trạng thái của khí lí tưởng
Khái niệm
Phương trình trạng thái của khí lí tưởng là một mô hình toán học dùng để mô tả mối quan hệ giữa áp suất, thể tích và nhiệt độ của một lượng khí lí tưởng trong điều kiện nhất định.
Khí lí tưởng là một mô hình lý tưởng trong đó các phân tử khí được giả định không có thể tích và không tương tác với nhau ngoại trừ khi va chạm. Mặc dù không có khí thực tế nào hoàn toàn tuân theo mô hình này, phương trình cung cấp một dự đoán chính xác đáng kể cho hành vi của hầu hết các khí ở áp suất thấp và nhiệt độ cao.
Công thức
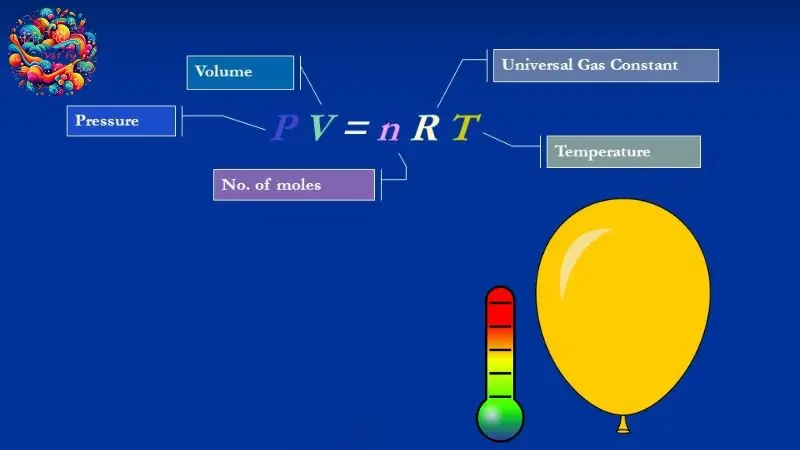
Phương trình trạng thái của khí lí tưởng được biểu diễn dưới dạng:
\[ PV = nRT \]
Trong đó:
– \( P \) là áp suất của khí (thường được đo bằng pascal, atm hoặc mmHg).
– \( V \) là thể tích mà khí chiếm giữ (thường được đo bằng lít hoặc mét khối).
– \( n \) là số mol của khí trong hệ thống.
– \( R \) là hằng số khí lí tưởng, có giá trị khoảng \( 8.314 \, \text{J/(mol·K)} \) hoặc \( 0.0821 \, \text{L·atm/(mol·K)} \), tùy thuộc vào đơn vị của áp suất và thể tích.
– \( T \) là nhiệt độ tuyệt đối của khí, đo bằng Kelvin.
Phương trình này thể hiện sự phụ thuộc lẫn nhau giữa áp suất, thể tích và nhiệt độ của khí lí tưởng, cho thấy khi một trong những đại lượng này thay đổi, ít nhất một trong hai đại lượng còn lại cũng sẽ thay đổi theo cách có thể dự đoán được để duy trì phương trình cân bằng.
Các dạng biến thể của phương trình
Phương trình trạng thái của khí lí tưởng có các dạng biến thể đặc biệt khi một trong các đại lượng (nhiệt độ, áp suất, hoặc thể tích) được giữ không đổi. Dưới đây là phân tích và công thức cho mỗi dạng biến thể:
Phương trình Boyle-Mariotte
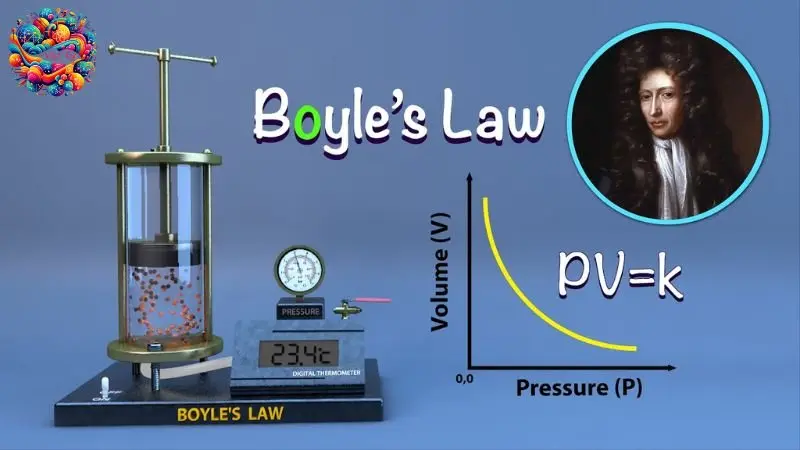
Khái niệm
Phương trình Boyle-Mariotte mô tả mối quan hệ giữa áp suất và thể tích của một lượng khí lí tưởng khi nhiệt độ được giữ không đổi.
Công thức
\[ P_1V_1 = P_2V_2 \]
Trong đó \( P_1 \) và \( V_1 \) là áp suất và thể tích ban đầu của khí, còn \( P_2 \) và \( V_2 \) là áp suất và thể tích sau khi có sự thay đổi.
Phương trình Charles
Khái niệm
Phương trình Charles mô tả mối quan hệ giữa thể tích và nhiệt độ của một lượng khí lí tưởng khi áp suất được giữ không đổi.
Công thức
\[ \frac{V_1}{T_1} = \frac{V_2}{T_2} \]
Ở đây \( V_1 \) và \( T_1 \) là thể tích và nhiệt độ ban đầu của khí, trong khi \( V_2 \) và \( T_2 \) là thể tích và nhiệt độ sau khi có sự thay đổi.
Phương trình Gay-Lussac
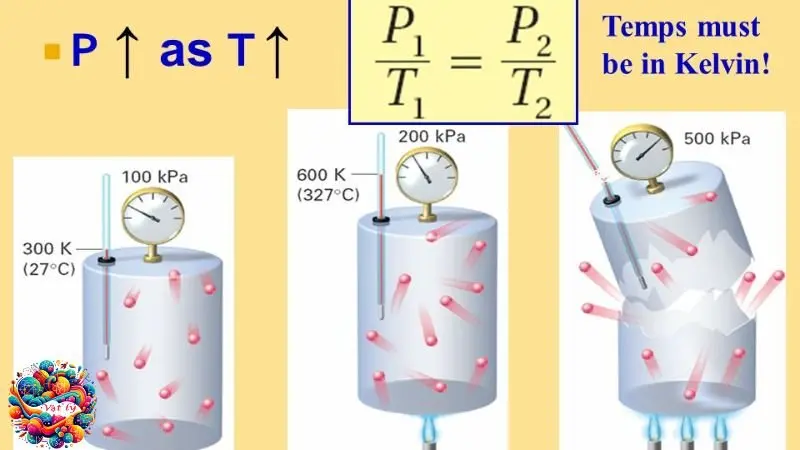
Khái niệm
Phương trình Gay-Lussac mô tả mối quan hệ giữa áp suất và nhiệt độ của một lượng khí lí tưởng khi thể tích được giữ không đổi.
Công thức
\[ \frac{P_1}{T_1} = \frac{P_2}{T_2} \]
Trong công thức này, \( P_1 \) và \( T_1 \) là áp suất và nhiệt độ ban đầu của khí, còn \( P_2 \) và \( T_2 \) là áp suất và nhiệt độ sau khi có sự thay đổi.
Mỗi phương trình này thể hiện một dạng biến thể của phương trình trạng thái khí lí tưởng, áp dụng cho các điều kiện cụ thể khi một trong các đại lượng được giữ cố định.
Sự hiểu biết về các mối quan hệ này giúp chúng ta có cái nhìn sâu sắc hơn về cách thức các đại lượng vật lý ảnh hưởng lẫn nhau trong hệ khí lí tưởng, cung cấp công cụ hữu ích trong việc giải quyết các vấn đề thực tế trong khoa học và kỹ thuật.
Ví dụ minh hoạ
Ví dụ 1: Một bình kín chứa khí lí tưởng có thể tích 2.0 L ở nhiệt độ 27°C và áp suất 1.0 atm. Tính thể tích của lượng khí này khi nhiệt độ tăng lên đến 127°C và áp suất giảm xuống còn 0.5 atm.
Hướng dẫn cách giải
Đầu tiên, chúng ta cần chuyển đổi nhiệt độ từ độ Celsius sang Kelvin bằng cách cộng với 273.15:
– Nhiệt độ ban đầu: \( T_1 = 27°C + 273.15 = 300.15 K \)
– Nhiệt độ sau khi tăng: \( T_2 = 127°C + 273.15 = 400.15 K \)
Sử dụng phương trình trạng thái của khí lí tưởng \( P_1V_1/T_1 = P_2V_2/T_2 \), ta có thể giải để tìm \( V_2 \), thể tích của khí ở trạng thái sau.
Chú ý rằng áp suất được đo bằng atm, nên không cần chuyển đổi sang đơn vị khác.
Thay thế các giá trị đã biết vào phương trình:
\[ \frac{1.0 \, \text{atm} \times 2.0 \, \text{L}}{300.15 \, \text{K}} = \frac{0.5 \, \text{atm} \times V_2}{400.15 \, \text{K}} \]
Giải phương trình để tìm \( V_2 \):
\[ V_2 = \frac{1.0 \, \text{atm} \times 2.0 \, \text{L} \times 400.15 \, \text{K}}{300.15 \, \text{K} \times 0.5 \, \text{atm}} \]
\[ V_2 = \frac{800.3}{150.075} \, \text{L} \]
\[ V_2 \approx 5.33 \, \text{L} \]
Vậy, thể tích của lượng khí trong bình ở nhiệt độ 127°C và áp suất 0.5 atm sẽ là 5.33 L.
Ví dụ 2: Một bóng bay được bơm khí helium có thể tích là 500 mL ở nhiệt độ phòng 25°C. Khi bóng bay được thả ra ngoài trời nóng lên đến nhiệt độ 35°C, hãy tính thể tích mới của bóng bay, giả sử áp suất không khí xung quanh không đổi.
Hướng dẫn cách giải
Để giải bài toán này, ta sử dụng phương trình Charles, vì áp suất giữ nguyên và chỉ có thể tích và nhiệt độ thay đổi: \( \frac{V_1}{T_1} = \frac{V_2}{T_2} \).
Bước 1: Chuyển đổi nhiệt độ từ Celsius sang Kelvin
– Nhiệt độ ban đầu \( T_1 = 25°C = 298K \) (vì \( 25 + 273 = 298 \))
– Nhiệt độ sau khi tăng \( T_2 = 35°C = 308K \) (vì \( 35 + 273 = 308 \))
Bước 2: Áp dụng phương trình Charles
Chúng ta biết \( V_1 = 500 \, \text{mL} \) và cần tìm \( V_2 \). Áp dụng phương trình Charles, ta có:
\[ \frac{500}{298} = \frac{V_2}{308} \]
Giải phương trình này để tìm \( V_2 \):
\[ V_2 = \frac{500 \times 308}{298} \]
\[ V_2 \approx 517 \, \text{mL} \]
Vậy, khi nhiệt độ tăng từ 25°C lên 35°C và áp suất không đổi, thể tích của bóng bay tăng lên và đạt khoảng 517 mL.
Hy vọng qua bài viết này, bạn đã có thêm kiến thức về phương trình trạng thái của khí lý tưởng. Hãy theo dõi vatly.edu.vn để tiếp tục khám phá và mở rộng hiểu biết về vật lý. Chúng tôi luôn sẵn lòng giải đáp thắc mắc và chia sẻ kiến thức với bạn.
