Điện trường và cường độ điện trường: Giải mã thế giới bí ẩn của lực điện

Chào mừng quý độc giả đến với vatly.edu.vn, nơi cập nhật các bài viết chất lượng cao về vật lý. Trong bài viết này, chúng ta sẽ khám phá một trong những khái niệm cơ bản nhất trong lĩnh vực điện từ học: điện trường và cường độ điện trường.

Đây là những yếu tố không chỉ quan trọng trong nghiên cứu khoa học mà còn ứng dụng rộng rãi trong các công nghệ hàng ngày. Cùng tìm hiểu về cách thức hoạt động của điện trường và cách chúng ảnh hưởng đến các hạt mang điện xung quanh chúng.

Khái niệm về điện trường

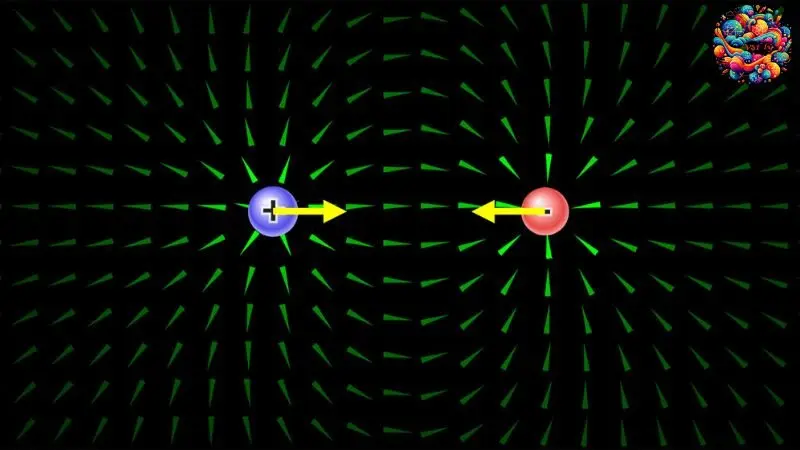
Điện trường là một thực thể vật lý hình thành xung quanh các điện tích và có khả năng truyền tải tương tác giữa chúng. Nó được tạo ra bởi sự hiện diện của điện tích và có chức năng chính là thực hiện lực điện đối với các điện tích khác khi chúng được đặt trong phạm vi ảnh hưởng của điện trường đó.

Đây là một trong những đặc tính cơ bản và quan trọng nhất của điện trường, giúp nó đóng vai trò chủ đạo trong các hiện tượng vật lý liên quan đến điện và từ.

Tìm hiểu về cường độ điện trường

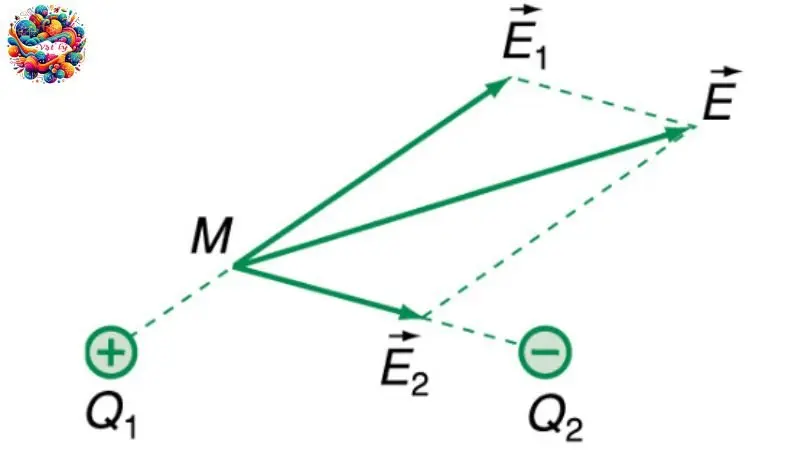
Cường độ điện trường là một đại lượng vật lý miêu tả mức độ mạnh yếu của một điện trường tại một điểm nhất định, dựa trên lực tác động lên điện tích thử đặt tại điểm đó. Để hiểu rõ hơn, cường độ điện trường có thể được biểu diễn qua một vectơ và tính toán theo công thức:

\[\large \vec{E}=\frac{\vec{F}}{q}\]

trong đó \(\vec{F}\) là lực điện tác dụng lên điện tích \(q\) tại điểm được xét.

Đối với một điện tích điểm \(Q\) đặt trong không khí hay chân không, cường độ điện trường tại một điểm cách điện tích \(Q\) một khoảng \(r\) có thể được tính bằng công thức:

\[\large E=\frac{\left | Q \right |}{4\pi \varepsilon_{o}r^{2}}\]

trong đó \(\varepsilon_{o}\) là hằng số điện môi của môi trường. Trong các môi trường điện môi, cường độ điện trường do \(Q\) tạo ra tại một điểm sẽ yếu hơn so với trong chân không do sự ảnh hưởng của môi trường lên sự phân bố trường điện.

Đường sức điện 

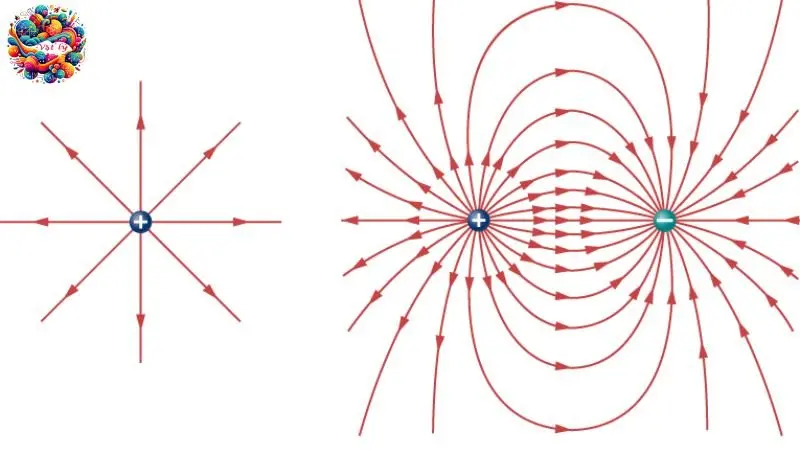
Điện phổ

Điện phổ được hiểu là hệ thống bao gồm các đường sức, mô tả cường độ của điện trường xung quanh các điện tích. Đây là công cụ hữu ích để trực quan hóa và phân tích cấu trúc của điện trường trong nghiên cứu và ứng dụng.

Khái niệm đường sức điện

Đường sức điện là mô hình hóa của điện phổ, dùng để miêu tả đường mà lực điện tác động. Tiếp tuyến tại bất kỳ điểm nào trên đường sức điện này sẽ có phương trùng với hướng của vectơ cường độ điện trường, cung cấp hình ảnh sinh động và dễ hiểu về sự phân bố lực điện trong không gian.

Đặc điểm của đường sức điện:

• Mỗi điểm trong điện trường chỉ có thể có một đường sức điện đi qua.
• Hướng của đường sức điện tại một điểm chính là hướng của vectơ cường độ điện trường tại điểm đó.
• Đường sức điện không phải là các đường kín; chúng bắt đầu từ điện tích dương và kết thúc tại điện tích âm, thể hiện rõ ràng sự chuyển động của lực điện từ cực dương sang cực âm.

Qua đây, việc hiểu và sử dụng khái niệm đường sức điện trở nên trực quan và hiệu quả hơn, giúp ta nhận biết và tính toán các tác động điện trong các môi trường khác nhau.

Điện trường đều

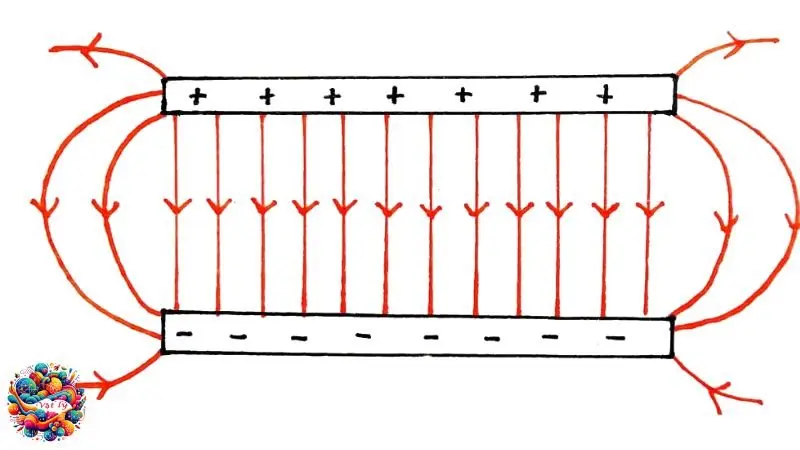
Điện trường đều là điện trường mà vectơ cường độ điện trường tại mọi điểm đều có cùng phương, cùng chiều, và cùng độ lớn.

Khái niệm điện trường đều

Điện trường đều là một loại điện trường mà tại mọi điểm trong nó, vectơ cường độ điện trường đều nhất quán về độ lớn và hướng. Đây là môi trường lý tưởng để nghiên cứu các hiện tượng điện do sự đồng nhất này. Trong một điện trường đều, các đường sức điện trường là những đường thẳng song song và cách đều nhau, cho thấy sự phân bố lực điện đồng đều trong không gian.

Điện trường đều giữa hai bản phẳng nhiễm điện đặt song song

Một ví dụ điển hình của điện trường đều là điện trường tạo thành giữa hai bản phẳng nhiễm điện đặt song song và mang điện trái dấu nhau. Cường độ điện trường trong không gian giữa hai bản này được tính bằng tỉ số giữa hiệu điện thế \(U\) và khoảng cách \(d\) giữa chúng:

\[\large E=\frac{U}{d}\]

Tác dụng của điện trường đều đối với chuyển động của một điện tích

Khi một điện tích chuyển động vào trong một điện trường đều, lực điện tác động lên nó sẽ hướng theo phương vuông góc với đường sức, làm thay đổi phương của vận tốc điện tích mà không ảnh hưởng đến tốc độ theo phương vuông góc với đường sức. Do đó, quỹ đạo của điện tích sẽ thay đổi phương và dần tăng tốc độ, tạo thành một đường cong trong không gian.

Những kiến thức về điện trường đều không chỉ là nền tảng cơ bản trong nghiên cứu vật lý mà còn có ứng dụng rộng rãi trong các thiết kế kỹ thuật và thiết bị điện tử, giúp chúng ta hiểu và tận dụng hiệu quả các hiện tượng tự nhiên xung quanh.

Bài tập ứng dụng về điện trường – Vật lý 11 (có đáp án)

Bài 1: Một điện tích điểm \(Q = +2 \times 10^{-6} \, \text{C}\) đặt tại không khí. Tính cường độ điện trường tại điểm M cách Q 0.3 m.

Hướng dẫn giải:

– Sử dụng công thức tính cường độ điện trường: 

\[ E = \frac{k \times |Q|}{r^2} \]

– Với \( k = 9 \times 10^9 \, \text{Nm}^2/\text{C}^2 \), \( Q = 2 \times 10^{-6} \, \text{C} \), và \( r = 0.3 \, \text{m} \).

Giải:

\[ E = \frac{9 \times 10^9 \times 2 \times 10^{-6}}{(0.3)^2} = 2 \times 10^5 \, \text{N/C} \]

Đáp án: \( E = 2 \times 10^5 \, \text{N/C} \)

Bài 2: Một điện tích điểm \( Q = -3 \times 10^{-6} \, \text{C} \) đặt tại không khí. Xác định hướng của điện trường tại điểm M cách Q 0.2 m.

Hướng dẫn giải:

– Điện trường xung quanh một điện tích âm hướng về phía điện tích.

Đáp án: Điện trường tại M hướng về phía điện tích Q.

Bài 3: Đặt một điện tích thử \( q = +1 \times 10^{-9} \, \text{C} \) vào một điện trường có cường độ \( E = 5 \times 10^4 \, \text{N/C} \). Tính lực điện tác dụng lên \( q \).

Hướng dẫn giải:

– Sử dụng công thức tính lực điện: 

\[ F = q \times E \]

– Thay số vào công thức: \( q = 1 \times 10^{-9} \, \text{C} \) và \( E = 5 \times 10^4 \, \text{N/C} \).

Giải:

\[ F = 1 \times 10^{-9} \times 5 \times 10^4 = 5 \times 10^{-5} \, \text{N} \]

Đáp án: \( F = 5 \times 10^{-5} \, \text{N} \)

Bài 4: Biết cường độ điện trường giữa hai điện tích điểm bằng nhau và bằng \( 1 \times 10^5 \, \text{N/C} \), điện tích mỗi điện tích là \( +5 \times 10^{-6} \, \text{C} \). Tính khoảng cách giữa hai điện tích.

Hướng dẫn giải:

– Cường độ điện trường do mỗi điện tích tạo ra tại điểm đặ

t điện tích kia là \( E = \frac{k \times |Q|}{r^2} \).

– Sử dụng công thức và giải phương trình để tìm \( r \).

Giải:

– Gọi \( r \) là khoảng cách cần tìm.

\[ 1 \times 10^5 = \frac{9 \times 10^9 \times 5 \times 10^{-6}}{r^2} \]

\[ r^2 = \frac{9 \times 10^9 \times 5 \times 10^{-6}}{1 \times 10^5} \]

\[ r = \sqrt{\frac{45 \times 10^3}{10^5}} \approx 0.21 \, \text{m} \]

Đáp án: Khoảng cách giữa hai điện tích là \( \approx 0.21 \, \text{m} \)

Qua bài viết này tại vatly.edu.vn, hy vọng bạn đã có thể nắm bắt được những kiến thức cơ bản về điện trường và cường độ điện trường. Những hiểu biết này không chỉ là nền tảng cho việc tiếp tục khám phá vật lý mà còn giúp bạn hiểu rõ hơn về ứng dụng của chúng trong công nghệ và đời sống, từ màn hình cảm ứng cho đến các thiết bị điện tử.

Hãy tiếp tục theo dõi và khám phá thêm nhiều bài viết thú vị khác về vật lý tại vatly.edu.vn, nơi tri thức không ngừng được mở rộng.