Vén màn bí mật về định luật bảo toàn năng lượng trong vật lý
Định luật bảo toàn năng lượng là một trong những nguyên lý cơ bản nhất của vật lý, đóng vai trò là nền tảng cho hiểu biết của chúng ta về thế giới tự nhiên. Từ các phản ứng hóa học trong phòng thí nghiệm đến quá trình sinh trưởng của vũ trụ, định luật này khẳng định rằng tổng lượng năng lượng trong một hệ thống đóng là một hằng số.
Bài viết này sẽ đi sâu vào giải thích định luật bảo toàn năng lượng, cùng với các ứng dụng và ví dụ minh họa giúp bạn hiểu rõ hơn về nguyên tắc quan trọng này.
Năng lượng là gì?

Năng lượng là một đại lượng vật lý mà phải được chuyển đến một đối tượng để thực hiện một công trên, hoặc để làm nóng, các đối tượng. Nó được xem là một đại lượng được bảo toàn; định luật bảo toàn năng lượng cho biết năng lượng có thể được chuyển đổi thành các dạng khác nhau, nhưng không tự nhiên sinh ra hoặc mất đi.
Nói đơn giản hơn, năng lượng là khả năng để làm việc. Nó có trong mọi thứ xung quanh chúng ta và cần thiết cho tất cả các khía cạnh đời sống. Cơ thể chuyển thức ăn thành năng lượng để duy trì cuộc sống cho chúng ta. Nhiên liệu cung cấp năng lượng cho xe chạy.
Năng lượng tồn tại dưới nhiều dạng khác nhau, bao gồm:
- Năng lượng cơ học: là năng lượng liên quan đến chuyển động của vật thể. Ví dụ: năng lượng của một quả bóng đang bay, năng lượng của một chiếc xe đang chạy.
- Năng lượng nhiệt: là năng lượng liên quan đến chuyển động nhiệt của các phân tử. Ví dụ: năng lượng của một cốc nước nóng, năng lượng của lửa.
- Năng lượng điện: là năng lượng liên quan đến chuyển động của các hạt điện. Ví dụ: năng lượng của một tia sét, năng lượng của một bóng đèn.
- Năng lượng hóa học: là năng lượng được lưu trữ trong các liên kết hóa học. Ví dụ: năng lượng của thức ăn, năng lượng của pin.
- Năng lượng hạt nhân: là năng lượng được giải phóng từ các phản ứng hạt nhân. Ví dụ: năng lượng của Mặt Trời, năng lượng của các nhà máy điện hạt nhân.
Cơ sở hình thành định luật bảo toàn năng lượng

Nền tảng của luật bảo toàn năng lượng có thể được hiểu qua các quá trình cơ bản sau:
Chuyển đổi giữa thế năng và động năng
Trước khi công nhận luật bảo toàn năng lượng, các quan sát đã chỉ ra sự chuyển đổi từ thế năng sang động năng và ngược lại. Trong nhiều hiện tượng tự nhiên, quá trình này được thể hiện một cách rõ ràng. Năng lượng vị trí hoặc thế năng có thể chuyển thành năng lượng chuyển động, trong khi một phần năng lượng cơ học có thể không được bảo toàn trong dạng cơ năng ban đầu.
Chuyển đổi giữa cơ năng và điện năng
Tương tự, khi xem xét sự biến đổi giữa cơ năng và điện năng, theo luật bảo toàn cơ năng, cơ năng có thể được chuyển đổi thành điện năng và ngược lại. Điều này được minh chứng rõ trong các động cơ điện, nơi điện năng được chuyển đổi thành năng lượng cơ học. Trong khi đó, máy phát điện làm điều ngược lại, chuyển hóa cơ năng thành điện năng.
Một điều đáng chú ý là khi một lượng cơ năng có sự gia tăng so với mức ban đầu, điều này chỉ ra rằng một dạng năng lượng khác đã được chuyển đổi và cung cấp năng lượng cho sự gia tăng đó.
Ai là người phát hiện ra định luật bảo toàn năng lượng?

Định luật bảo toàn năng lượng, một trong những nguyên lý cơ bản nhất của vật lý, được hiểu rằng tổng năng lượng trong một hệ cô lập là không đổi theo thời gian. Người ta thường gán công trình này cho James Prescott Joule, một nhà vật lý Anh, qua thí nghiệm của ông vào năm 1845, chứng minh sự chuyển hóa năng lượng từ công thành nhiệt năng và đặt nền móng cho định luật này.
Ngoài Joule, Julius Mayer, một bác sĩ và nhà vật lý học người Đức, cũng đóng góp quan trọng cho định luật bảo toàn năng lượng. Ông đã phân tích các trường hợp cụ thể của việc chuyển hóa năng lượng và tìm ra cách tính đương lượng cơ của nhiệt, mở rộng tư duy về chuyển hóa năng lượng trong vũ trụ.
Hermann Ludwig Ferdinand von Helmholtz, một bác sỹ và nhà vật lý người Đức khác, cũng khám phá ra định luật bảo toàn và chuyển hóa năng lượng khi nghiên cứu về sự trao đổi chất của cơ bắp và phủ nhận giả thuyết về “lực sống” cần thiết cho sự chuyển động của cơ bắp.
Helmholtz mở rộng phạm vi của nguyên lý bảo toàn năng lượng và phát triển nó dựa trên cơ sở thực nghiệm.
Như vậy, định luật bảo toàn năng lượng là kết quả của những nỗ lực nghiên cứu và phát triển liên tục của nhiều nhà khoa học, và không thể gán công trình này cho một cá nhân duy nhất.
Các công thức liên quan định luật bảo toàn năng lượng

Định luật bảo toàn năng lượng nêu rõ rằng trong một hệ kín, tổng năng lượng luôn được bảo toàn. Dưới đây là một số công thức và biểu thức liên quan đến định luật này trong các tình huống khác nhau:
Công thức tính Công
W = F⋅d⋅cos(θ)
Trong đó:
- W là công thực hiện
- F là lực tác dụng
- d là khoảng cách di chuyển
- θ là góc giữa vectơ lực và vectơ di chuyển
Công suất trung bình
Pavg = W/t
Trong đó:
- Pavg là công suất trung bình
- W là công thực hiện trong thời gian
Công suất tức thời
P = F⋅v
Trong đó:
- P là công suất tức thời,
- F là lực tác dụng,
- v là vận tốc của vật.
Động năng

K= ½ mv2
Trong đó:
- K là động năng
- m là khối lượng của vật
- v là vận tốc của vật.
Liên hệ giữa động năng và công
W = ΔK
Trong đó:
- W là công thực hiện bởi lực ngoại lực,
- ΔK là sự thay đổi động năng.
Thế năng trọng trường
U = mgh
Trong đó:
- U là thế năng trọng trường
- m là khối lượng
- g là gia tốc trọng trường
- h là độ cao so với mặt đất
Liên hệ giữa thế năng trọng trường và công
W = −ΔU
Trong đó:
- W là công thực hiện bởi trọng lực
- ΔU là sự thay đổi thế năng trọng trường
Công của trọng lực (rơi)
W = mgh
*Tương tự như thế năng trọng trường, công của trọng lực khi rơi tự do cũng được tính bằng mgh.
Thế năng đàn hồi
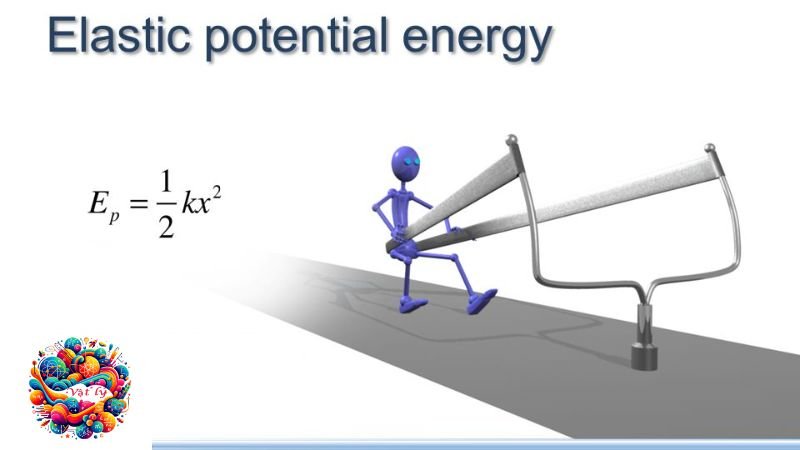
U = ½ kx²
Trong đó:
- U là thế năng đàn hồi,
- k là hệ số đàn hồi của lò xo,
- x là độ biến dạng của lò xo so với trạng thái ban đầu.
Liên hệ giữa thế năng đàn hồi và công
W = ½ kx²
* Công để biến dạng lò xo cũng chính là thế năng đàn hồi mà lò xo tích lũy.
Cơ năng
E = K+U
Trong đó: E là tổng cơ năng (động năng cộng thế năng).
Định luật bảo toàn cơ năng

W = Wđ + Wt
Trong đó:
- Wđ là động năng của hệ, phụ thuộc vào vận tốc của các vật trong hệ.
- Wt là thế năng của hệ, phụ thuộc vào vị trí và trạng thái của các vật trong hệ.
Độ cao động năng bằng n lần thế năng
h = n.h’
Trong đó:
- h: Độ cao mà tại đó vật có động năng bằng n lần thế năng.
- n: Hệ số, là số lần động năng lớn hơn thế năng.
- h’: Độ cao mà tại đó vật có động năng bằng thế năng.
Hiệu suất
H = Aci/A = Wci/W (η)
Trong đó:
- H: Hiệu suất (không có đơn vị)
- Aci: Công có ích (J)
- A: Công toàn phần (J)
- Wci: Năng lượng có ích (J)
- W: Năng lượng toàn phần (J)
- η: Ký hiệu của hiệu suất
Bài tập về định luật bảo toàn năng lượng

Bài 1: Một viên bi có khối lượng 0,5 kg được thả rơi từ độ cao 10 m so với mặt đất. Bỏ qua sức cản của không khí.
a) Tính động năng của viên bi khi ở độ cao 5 m.
b) Tính vận tốc của viên bi khi chạm đất.
Đáp án:
a) Động năng của viên bi khi ở độ cao 5m là:
Wđ = ½mv² = ½ * 0,5 * (√(2gh))² = ½ * 0,5 * (√(2 * 9,8 * 5))² = 12,25 J
b) Vận tốc của viên bi khi chạm đất là:
v = √(2gh) = √(2 * 9,8 * 10) = 14 m/s
Bài 2: Một con lắc lò xo có độ cứng k = 100 N/m, khối lượng m = 1 kg. Kéo con lắc lò xo ra khỏi vị trí cân bằng một đoạn 10cm và thả nhẹ.
a) Tính thế năng đàn hồi của con lắc lò xo khi ở vị trí bị nén 5 cm.
b) Tính vận tốc của con lắc lò xo khi đi qua vị trí cân bằng.
Đáp án:
a) Thế năng đàn hồi của con lắc lò xo khi ở vị trí bị nén 5cm là:
Wt = ½kx² = ½ * 100 * (0,05)² = 1,25 J
b) Vận tốc của con lắc lò xo khi đi qua vị trí cân bằng là:
v = √(k/m) * x = √(100/1) * 0,1 = √10 = 3,16 m/s
Bài 3: Một bóng đèn có công suất 100 W được sử dụng trong 3 giờ. Tính điện năng tiêu thụ của bóng đèn.
Đáp án:
Điện năng tiêu thụ của bóng đèn là:
A = Pt = 100 * 3 = 300 Wh = 0,3 kWh
Bài 4: Một động cơ điện có hiệu suất 80%. Khi động cơ hoạt động trong 1 giờ, nó tiêu thụ điện năng là 1,2 kWh. Tính công mà động cơ thực hiện được.
Đáp án:
Công mà động cơ thực hiện được là:
A = Hiệu suất * A = 0,8 * 1,2 = 0,96 kWh = 3456 kJ
Bài 5: Một ô tô có khối lượng 1 tấn đang chạy với vận tốc 36 km/h. Tính động năng của ô tô.
Đáp án:
Động năng của ô tô là:
Wđ = ½mv² = ½ * 1000 * (36 * 1000/3600)² = 400000 J
Từ việc khám phá sâu xa định luật bảo toàn năng lượng, chúng ta có thể thấy rõ tầm quan trọng của nó trong mọi lĩnh vực của khoa học và kỹ thuật.
Nguyên lý này không chỉ giúp chúng ta giải thích nhiều hiện tượng tự nhiên mà còn là chìa khóa trong việc phát triển các công nghệ mới, từ tái tạo năng lượng đến cải tiến hiệu suất trong công nghiệp.
Hy vọng rằng, qua bài viết này, bạn đã có thêm kiến thức về định luật bảo toàn năng lượng và nhận thức được giá trị áp dụng của nó trong cuộc sống hàng ngày cũng như trong tương lai của nhân loại.







